Puzzles
11 December
Two more than today's number is the reverse of two times today's number.
10 December
How many zeros does 1000! (ie 1000 × 999 × 998 × ... × 1) end with?
9 December
Write the numbers 1 to 15 in a row. Underneath, write the same list without the first and last numbers. Continue this until you have just one number left.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||||
| etc. | ||||||||||||||
Today's number is the sum of all the numbers you have written.
8 December
The odd numbers are written in a pyramid.
| 1 | ||||
| 3 | 5 | |||
| 7 | 9 | 11 | ||
| etc. | ||||
What is the mean of the numbers in the 23rd row?
7 December
The odd numbers are written in a pyramid.
| 1 | ||||
| 3 | 5 | |||
| 7 | 9 | 11 | ||
| etc. | ||||
What is the sum of the numbers in the seventh row?
6 December
\(p(x)\) is a quadratic with real coefficients. For all real numbers \(x\),
$$x^2+4x+14\leq p(x)\leq 2x^2+8x+18$$
\(p(2)=34\). What is \(p(6)\)?
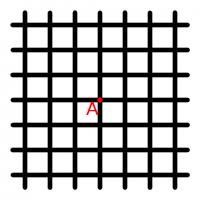
5 December
You start at A and are allow to walk left, right, up or down along the grid. The grid continues forever in every direction. After you have walked thirteen units, how many different locations could you be in?
4 December
Pick a three digit number whose digits are all different.
Sort the digits into ascending and descending order to form two new numbers. Find the difference between these numbers.
Repeat this process until the number stops changing. The final result is today's number.