Puzzles
3 December
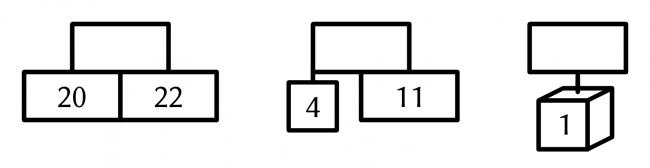
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10. Today's number is the product of the numbers in the red boxes.
| + | | + | | = 17 |
| + | | ÷ | | × | |
| ÷ | | - | | = 1 |
| - | | × | | ÷ | |
| ÷ | | - | | = 0 |
=
4 | | =
12 | | =
27 | |
2 December
There are three cards; one number is written on each card. You are told that the sums of pairs of cards are 99, 83 and 102.
What is the sum of all three cards?
Show answer
Hide answer
Adding up all three sums of pairs (284) will give twice the sum of the three numbers. So the sum of the three numbers is 142.
1 December
Today's number is the smallest three digit number such that the sum of its digits is equal to the product of its digits.
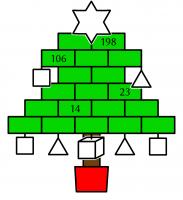
What's the star?
In the Christmas tree below, the rectangle, baubles, and the star at the top each contain a number. The square baubles contain square numbers; the triangle baubles contain triangle numbers; and the cube bauble contains a cube number.
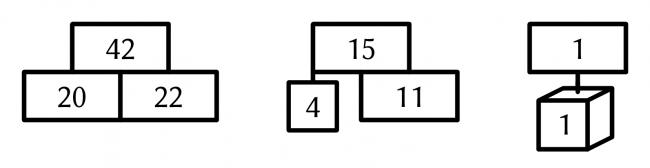
The numbers in the rectangles (and the star) are equal to the sum of the numbers below them. For example, if the following numbers are filled in:
then you can deduce the following:
What is the number in the star at the top of this tree?
You can download a printable pdf of this puzzle here. Show answer
Hide answer
The two numbers between 14 are a cube number and a triangle number: these must be 8 and 6. Next you can see that 23 is the sum of 8, two times a triangle number and a square number: the triangle and square numbers must be 3 and 9.
Next, call the square number at the bottom left \(a\), the square number at the top left \(b\), and the triangle number at the top right \(c\). Adding upwards, we find that \(a+b+45=106\) and \(a+141+c=198\); and so \(a+b=61\) and \(a+c=57\). The only two square numbers that add to 61 are 25 and 36. Therefore \(c\) must be 21 or 32, but must be 21 as 32 is not a triangle number. And so \(a\) is 36 and \(b\) is 25.
Putting all these numbers into the tree gives the top number as
433. This is fitting because 433 is in fact a
star number:

XYZ
Which digits \(X\), \(Y\) and \(Z\) fill this sum?
$$
\begin{array}{cccc}
&X&Z&Y\\
+&X&Y&Z\\
\hline
&Y&Z&X
\end{array}
$$
Show answer & extension
Hide answer & extension
Both the units and tens columns contain \(Y+Z\). The results are different (\(X\) and \(Z\)), so \(Y+Z=X+10\) and \(Z=X+1\) (because the 1 carries into the next column).
Therefore, \(Y+X+1 = X+10\), so \(Y=9\).
From the hundreds column, we see that \(X+X+1=Y\), so \(X=4\) and \(Z=5\).
Extension
Which digits \(X\), \(Y\) and \(Z\) fill this sum?
$$
\begin{array}{cccc}
&X&Z&Y\\
+&X&Y&Z\\
\hline
&Z&Y&X
\end{array}
$$
Where is Evariste?
Evariste is standing in a rectangular formation, in which everyone is lined up in rows and columns. There are 175 people in all the rows in front of Evariste and 400 in the rows behind him. There are 312 in the columns to his left and 264 in the columns to his right.
In which row and column is Evariste standing?
Show answer & extension
Hide answer & extension
The common factors of 175 and 400 are 1, 5, 25. Hence in front and behind him there are either:
| In front | Behind |
| 175 rows of 1 | 400 rows of 1 |
| 35 rows of 5 | 80 rows of 5 |
| 7 rows of 25 | 16 rows of 25 |
Therefore the shape of the formation is either 716×1, 126×5, or 24×25.
The length of the columns (716, 126, or 24) must be a factor of 312 and 264. Therefore it is 24.
Evariste is standing in the 8th row from the front and the 14th column from the left.
Extension
Evariste is standing in a rectangular formation, in which everyone is lined up in rows and columns. There are \(a\) people in all the rows in front of Evariste and \(b\) in the rows behind him. There are \(c\) in the columns to his left and \(d\) in the columns to his right.
For which numbers \(a\), \(b\), \(c\) and \(d\) is the row and column in which Evariste standing uniquely determined?
Bending a straw
Two points along a drinking straw are picked at random. The straw is then bent at these points. What is the probability that the two ends meet up to make a triangle?
Show answer & extension
Hide answer & extension
A triangle will be made if none of the segments of straw is longer than the other two added together. This is the same as requiring that each segment must be less than half the straw.
Let the length of the straw be 1 unit. Call the points \(x\) and \(y\). A triangle is made if either:
- \(x\lt y\), \(x\lt\tfrac12\), \(y-x\lt\tfrac12\), \(1-y\lt\tfrac12\); or
- \(y\lt x\), \(y\lt\tfrac12\), \(x-y\lt\tfrac12\), \(1-x\lt\tfrac12\).
For the second condition, the allowable region is shown below.
This region covers \(\tfrac18\) of the whole square. By switching \(x\) and \(y\) it can be seen that the first condition's region is the same size as the second's, plus they don't overlap. Therefore the probability of making a triangle is \(\tfrac18+\tfrac18=\tfrac14\).
Extension
One point along a drinking straw is picked, then a coin is flipped. If the coin shows heads, a second point above the first is chosen; If tails, a second point below the first is chosen. The straw is then bent at these points. What is the probability that the two ends meet up to make a triangle?
Turning squares
Each square on a chessboard contains an arrow point up, down, left or right. You start in the bottom left square. Every second you move one square in the direction shown by the arrow in your square. Just after you move, the arrow on the square you moved from rotates 90° clockwise. If an arrow would take you off the edge of the board, you stay in that square (the arrow will still rotate).
You win the game if you reach the top right square of the chessboard. Can I design a starting arrangement of arrows that will prevent you from winning?
Show answer
Hide answer
No, I can't.
If I could, then my arrangement would cause you to follow an infinitely long pattern without visiting this pattern. As there are only a finite number of squares, within this pattern there must be a square that you visit infinitely often. The arrow on this square will point in each direction an infinite number of times, so you must also visit the squares next to this one infinitely often.
For the same reason, you must visit the squares next to them infinitely often, and the squares next to them, and so on. In this way, we see that you visit every square, including the all-important winning square, infinitely often.