Puzzles
22 December
In bases 3 to 9, the number 112 is:
\(11011_3\),
\(1300_4\),
\(422_5\),
\(304_6\),
\(220_7\),
\(160_8\), and
\(134_9\).
In bases 3, 4, 6, 8 and 9, these representations contain no digit 2.
There are two 3-digit numbers that contain no 2 in their representations in all the bases between 3 and 9 (inclusive). Today's number is the smaller of these two numbers.
21 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the smallest number you can make with the digits in the red boxes.
| + | - | = 7 | |||
| ÷ | - | ÷ | |||
| + | ÷ | = 8 | |||
| × | × | × | |||
| + | - | = 7 | |||
| = 12 | = 5 | = 28 |
20 December
The integers from 2 to 14 (including 2 and 14) are written on 13 cards (one number per card). You and a friend take it in turns to take one of the numbers.
When you have both taken five numbers, you notice that the product of the numbers you have collected is equal to the product of the numbers that your friend has collected.
What is the product of the numbers on the three cards that neither of you has taken?
19 December
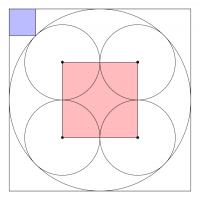
The diagram below shows three squares and five circles.
The four smaller circles are all the same size, and the red square's vertices are the centres of these circles.
The area of the blue square is 14 units. What is the area of the red square?
18 December
The final round of game show starts with £1,000,000. You and your opponent take it in turn to take any value between £1 and £900.
At the end of the round, whoever takes the final pound gets to take the money they have collected home, while the other player leaves with nothing.
You get to take an amount first. How much money should you take to be certain that you will not go home with nothing?
17 December
Eve picks a three digit number then reverses its digits to make a second number. The second number is larger than her original number.
Eve adds her two numbers together; the result is 584. What was Eve's original number?
16 December
Arrange the digits 1-9 in a 3×3 square so that:
the median number in the first row is 6;
the median number in the second row is 3;
the mean of the numbers in the third row is 4;
the mean of the numbers in the second column is 7;
the range of the numbers in the third column is 2,
The 3-digit number in the first column is today's number.
| median 6 | |||
| median 3 | |||
| mean 4 | |||
| today's number | mean 7 | range 2 |
15 December
There are 5 ways to make 30 by multiplying positive integers (including the trivial way):
- 30
- 2×15
- 3×10
- 5×6
- 2×3×5
Today's number is the number of ways of making 30030 by multiplying.