Advent calendar 2019
19 December
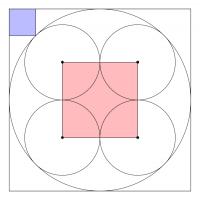
The diagram below shows three squares and five circles.
The four smaller circles are all the same size, and the red square's vertices are the centres of these circles.
The area of the blue square is 14 units. What is the area of the red square?
Show answer
Hide answer
The diagonal of the blue square is \(\sqrt{28}\). The radius \(R\) of the large circle satisfies \(R^2+R^2=(R+\sqrt{28})^2\).
Solving this, we find that \(R=\frac{\sqrt{28}}{\sqrt2-1}=\sqrt{28}(\sqrt2+1)\).
The radius \(r\) of the small circles satisfies \(r+r\sqrt2=R\), and so \(r=\frac{\sqrt{28}(\sqrt2+1)}{\sqrt2+1}=\sqrt{28}\).
The area of the square is \(4r^2=4\left(\sqrt{28}\right)^2=4\times28\). This is 112.
![](javascript:showlimage("advent2019circles.png"))