Puzzles
Two triangles
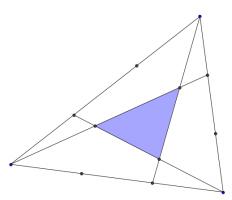
The three sides of this triangle have been split into three equal parts and three lines have been added.
What is the area of the smaller blue triangle as a fraction of the area of the original large triangle?
Show answer & extension
Hide answer & extension
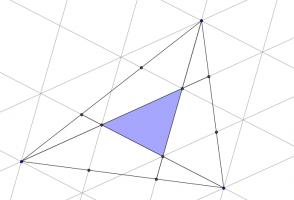
Draw on the following lines parallel to those which were added in the question.
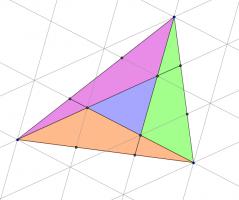
Then a grid of copies of the smaller blue triangle has been created. Now consider the three triangles which are coloured green, purple and orange in the following diagram:
Each of these traingles covers half a parallelogram made from four blue triangles. Therefore the area of each of these triangles is twice the area of the small blue triangle.
And so the blue triangle covers one seventh of the large triangle.
Extension
If the sides of the triangle were split into \(n\) pieces the the lines added, what would the area of the smaller blue triangle be as a fraction of the area of the original large triangle?
Equal side and angle
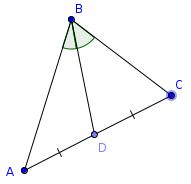
In the diagram shown, the lengths \(AD = CD\) and the angles \(ABD=CBD\).
Prove that the lengths \(AB=BC\).
Show answer
Hide answer
By the sine rule in BCD:
$$\frac{CD}{\sin(CBD)}=\frac{BD}{\sin(BCD)}$$
By the sine rule in BAD:
$$\frac{AD}{\sin(ABD)}=\frac{BD}{\sin(BAD)}$$
\(ABD=CBD\) and \(AD=CD\), so:
$$\sin(BAD)=\frac{BD\sin(ABD)}{AD}\\
=\frac{BD\sin(CBD)}{CD}\\
=\sin(BCD)$$
Using the sine rule in ABC:
$$\frac{AB}{\sin(BCD)}=\frac{BC}{\sin(BAD)}$$
The two sines are equal and so:
$$AB=BC$$
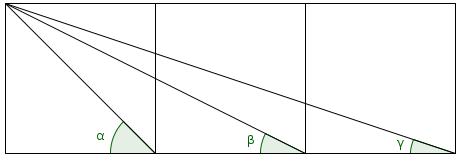
Arctan
Prove that \(\arctan(1)+\arctan(2)+\arctan(3)=\pi\).
Show answer & extension
Hide answer & extension
Let \(\alpha=\arctan(1)\), \(\beta=\arctan(2)\) and \(\gamma=\arctan(3)\), then draw the angles as follows:
Extension
Can you find any other integers \(a\), \(b\) and \(c\) such that:
$$\arctan(a)+\arctan(b)+\arctan(c)=\pi$$
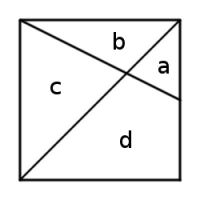
Square deal
This unit square is divided into four regions by a diagonal and a line that connects a vertex to the midpoint of an opposite side. What are the areas of the four regions?
Show answer & extension
Hide answer & extension
The square is unit, so \(a+b+c+d=1\). By the definitions of the lines, \(a+d=\frac{1}{2}\) and \(a+b=\frac{1}{4}\).
\(a\) and \(c\) are similar triangles. The vertical side of \(c\) is twice that of \(a\) so \(c=4a\).
Therefore we have the system of simultaneous equations:
$$a+b+c+d=1\\a+d=\frac{1}{2}\\a+b=\frac{1}{4}\\c=4a$$
These can be solved to find:
$$a=\frac{1}{12}\\b=\frac{1}{6}\\c=\frac{1}{3}\\d=\frac{5}{12}\\$$
Extension
What would be the areas if the lines were a diagonal and another line which divides the sides in the ratio \(x:y\)?
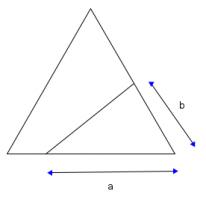
Half an equilateral triangle
What is the shortest straight line which bisects an equilateral triangle?
Show answer & extension
Hide answer & extension
Consider a line which bisects an equilateral triangle with sides of length 1. Let the sides of the smaller triangle created be \(a\) and \(b\) as shown below:
The area of the equilateral triangle is:
$$\frac{1}{2}\times 1\times 1\times \sin(60)\\=\frac{\sqrt{3}}{4}$$
The area of the smaller triangle is:
$$\frac{1}{2}ab \sin(60)\\=\frac{ab\sqrt{3}}{4}$$
This is half the area of the equilateral triangle, so:
$$ab=\frac{1}{2}$$
The length (\(L\)) of the line bisecting the equilateral triangle is:
$$L=a^2+b^2-2ab\cos(60)\\
=a^2+\left(\frac{1}{2a}\right)^2-\frac{2a}{2a}\times \frac{1}{2}\\
=a^2+\frac{1}{4a^2}-\frac{1}{2}$$
To find the minimum, we set the derivative to 0:
$$0=\frac{dL}{da}=2a-\frac{1}{2a^3}\\
4a^4-1=0\\
a^4=\frac{1}{4}\\
a=\frac{1}{\sqrt{2}}$$
For this value of \(a\), \(b\) and \(L\) also equal to \(\frac{1}{\sqrt{2}}\).
Extension
What if the line does not need to be straight?
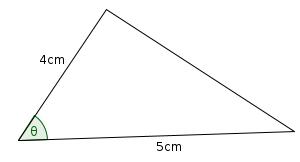
Largest triangle
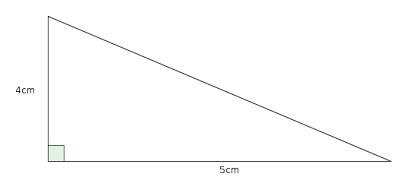
What is the largest area triangle which has one side of length 4cm and one of length 5cm?
Show answer & extension
Hide answer & extension
As our shape is a triangle, the 4cm and 5cm sides must be adjacent. Call the angle between them be \(\theta\).
The area of the triangle is \(\frac{1}{2}\times 4\times 5 \times \sin{\theta}\) or \(10\sin{\theta}\). This has a maximum value when \(\theta=90^\circ\), so the largest triangle has and area of 10cm2 and looks like:
Extension
What is the largest area triangle with a perimeter of 12cm?
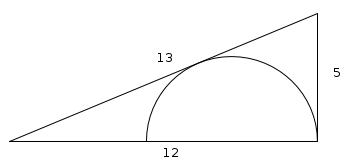
Semi circle in a triangle
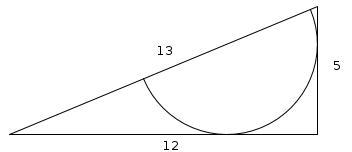
This right-angled triangle above has sides of lengths 12cm, 5cm and 13cm. The diameter of the semicircle lies on the 12cm side and the 13cm side is a tangent to the circle. What is the radius of the semi circle?
Show answer & extension
Hide answer & extension
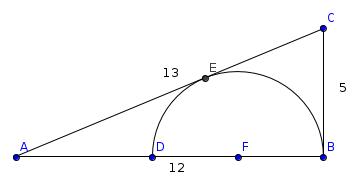
Label the triangle as follows:
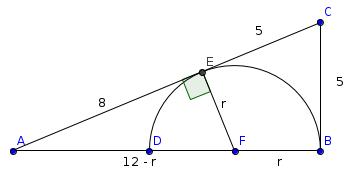
EC and BC are both tangents to the circle so FEA is a right angle and the lengths EC and BC are equal, so the length of EC is 5. Let r be the radius of the circle.
Using Pythagoras' Theorem in triangle FEA:
$$8^2+r^2=(12-r)^2$$
$$64+r^2=144-24r+r^2$$
$$24r=80$$
$$r=\frac{80}{24}=\frac{10}{3}$$
Extension
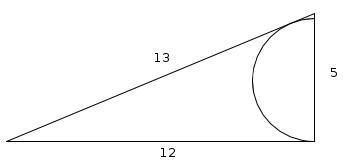
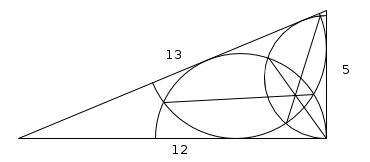
What is the radius of the circle whose diameter lies on the 5cm side and to which the 12cm and 13cm sides are tangents?
What is the radius of the circle whose diameter lies on the 13cm side and to which the 12cm and 5cm sides are tangents?
Additional observation
For each pair of semi circles, draw a straight line between the two points where the semi circles intersect. These lines all meet at a point.
Equal areas
An equilateral triangle and a square have the same area. What is the ratio of the perimeter of the triangle to the perimeter of the square?
Show answer & extension
Hide answer & extension
Let \(A\) be the area of the square (and the triangle).
The length of a side of the square is \(\sqrt{A}\), so the perimeter of the square is \(4\sqrt{A}\).
Let \(l\) be the length of a side the triangle. Then \(\frac{1}{2}l^2\sin{60}=A\), so \(l^2=\frac{4A}{\sqrt{3}}\). Therefore \(l=\frac{2\sqrt{A}}{3^\frac{1}{4}}\) and the perimeter of the triangle is \(\frac{6\sqrt{A}}{3^\frac{1}{4}}\).
Hence the ratio of the perimeters is \(\frac{6\sqrt{A}}{3^\frac{1}{4}} : 4\sqrt{A}\) which simplifies to 33/4:2
Extension
If an \(n\) sided regular polygon has the area \(A\), what is the length of one of its sides?
![](javascript:showlimage("two triangles.png"))
![](javascript:showlimage("two-tri-ans1.png"))
![](javascript:showlimage("two-tri-ans2.png"))
![](javascript:showlimage("equal-side-and-angle.png"))
![](javascript:showlimage("three-squares.png"))
![](javascript:showlimage("square-deal.png"))
![](javascript:showlimage("bisecting-equilateral.png"))
![](javascript:showlimage("triangle.png"))
![](javascript:showlimage("triangle-biggest.png"))
![](javascript:showlimage("circle-and-triangle.png"))
![](javascript:showlimage("labelled-tricirc.png"))
![](javascript:showlimage("labelled-tricirc2.png"))
![](javascript:showlimage("ext1.png"))
![](javascript:showlimage("ext2.png"))
![](javascript:showlimage("ext3.png"))