Puzzles
1 December
Today's number is the smallest three digit number such that the sum of its digits is equal to the product of its digits.
What's the star?
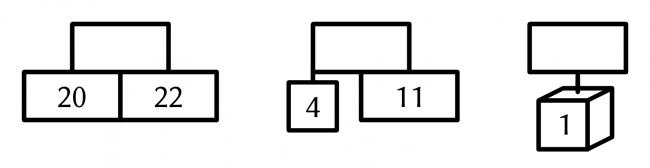
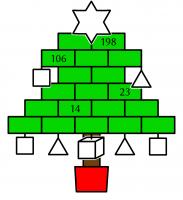
In the Christmas tree below, the rectangle, baubles, and the star at the top each contain a number. The square baubles contain square numbers; the triangle baubles contain triangle numbers; and the cube bauble contains a cube number.
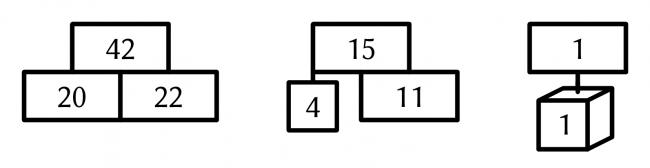
The numbers in the rectangles (and the star) are equal to the sum of the numbers below them. For example, if the following numbers are filled in:
then you can deduce the following:
What is the number in the star at the top of this tree?
You can download a printable pdf of this puzzle here. Show answer
Hide answer
The two numbers between 14 are a cube number and a triangle number: these must be 8 and 6. Next you can see that 23 is the sum of 8, two times a triangle number and a square number: the triangle and square numbers must be 3 and 9.
Next, call the square number at the bottom left \(a\), the square number at the top left \(b\), and the triangle number at the top right \(c\). Adding upwards, we find that \(a+b+45=106\) and \(a+141+c=198\); and so \(a+b=61\) and \(a+c=57\). The only two square numbers that add to 61 are 25 and 36. Therefore \(c\) must be 21 or 32, but must be 21 as 32 is not a triangle number. And so \(a\) is 36 and \(b\) is 25.
Putting all these numbers into the tree gives the top number as
433. This is fitting because 433 is in fact a
star number:

XYZ
Which digits \(X\), \(Y\) and \(Z\) fill this sum?
$$
\begin{array}{cccc}
&X&Z&Y\\
+&X&Y&Z\\
\hline
&Y&Z&X
\end{array}
$$
Show answer & extension
Hide answer & extension
Both the units and tens columns contain \(Y+Z\). The results are different (\(X\) and \(Z\)), so \(Y+Z=X+10\) and \(Z=X+1\) (because the 1 carries into the next column).
Therefore, \(Y+X+1 = X+10\), so \(Y=9\).
From the hundreds column, we see that \(X+X+1=Y\), so \(X=4\) and \(Z=5\).
Extension
Which digits \(X\), \(Y\) and \(Z\) fill this sum?
$$
\begin{array}{cccc}
&X&Z&Y\\
+&X&Y&Z\\
\hline
&Z&Y&X
\end{array}
$$
Where is Evariste?
Evariste is standing in a rectangular formation, in which everyone is lined up in rows and columns. There are 175 people in all the rows in front of Evariste and 400 in the rows behind him. There are 312 in the columns to his left and 264 in the columns to his right.
In which row and column is Evariste standing?
Show answer & extension
Hide answer & extension
The common factors of 175 and 400 are 1, 5, 25. Hence in front and behind him there are either:
| In front | Behind |
| 175 rows of 1 | 400 rows of 1 |
| 35 rows of 5 | 80 rows of 5 |
| 7 rows of 25 | 16 rows of 25 |
Therefore the shape of the formation is either 716×1, 126×5, or 24×25.
The length of the columns (716, 126, or 24) must be a factor of 312 and 264. Therefore it is 24.
Evariste is standing in the 8th row from the front and the 14th column from the left.
Extension
Evariste is standing in a rectangular formation, in which everyone is lined up in rows and columns. There are \(a\) people in all the rows in front of Evariste and \(b\) in the rows behind him. There are \(c\) in the columns to his left and \(d\) in the columns to his right.
For which numbers \(a\), \(b\), \(c\) and \(d\) is the row and column in which Evariste standing uniquely determined?
Elastic numbers
Throughout this puzzle, expressions like \(AB\) will represent the digits of a number, not \(A\) multiplied by \(B\).
A two-digit number \(AB\) is called elastic if:
- \(A\) and \(B\) are both non-zero.
- The numbers \(A0B\), \(A00B\), \(A000B\), ... are all divisible by \(AB\).
There are three elastic numbers. Can you find them?
Show answer & extension
Hide answer & extension
15, 18 and 45 are elastic.
15's factors are 5 and 3. 105, 1005, 10005, etc will all be multiples of 5 (because they end in 5) and multiples of 3 (as their digits add to 6). Hence they are all multiples of 15.
Similarly, 108, 1008, 10008, etc are all multiples of 9 (adding digits) and 2 (they are even), so they are multiples of 18; and 405, 4005, 40005, etc are all multiples of 9 (adding digits) and 5 (last digits are 5), so they are multiples of 45.
Extension
How many elastic numbers are there in other bases?
Square pairs
Source: Maths Jam
Can you order the integers 1 to 16 so that every pair of adjacent numbers adds to a square number?
For which other numbers \(n\) is it possible to order the integers 1 to \(n\) in such a way?
Show answer
Hide answer
Yes: 8, 1, 15, 10, 6, 3, 13, 12, 4, 5, 11, 14, 2, 7, 9, 16.
It is clearly possible for the numbers 1 to 15 (remove the 16 from the end of the sequence above) and 1 to 17 (add 17 to the start of the sequence above).
The OEIS sequence
A090461 gives other numbers for which this is possible. It starts 15, 16, 17, 23, then includes every number from 25 onwards. It is conjectured, but not proven, that it is possible for every number above 25.
Factorial pattern
$$1\times1!=2!-1$$
$$1\times1!+2\times2!=3!-1$$
$$1\times1!+2\times2!+3\times3!=4!-1$$
Does this pattern continue?
Show answer
Hide answer
Yes. It can be shown by induction:
First it's easy to check that \(1\times1!=2!-1\). Next assume that \(1\times1!+2\times2!+...+k\times k!=(k+1)!-1\). Now we try to show the pattern holds for \(k+1\).
$$1\times1!+2\times2!+...+k\times k!+(k+1)\times(k+1)!$$$$=(k+1)!-1+(k+1)\times(k+1)!$$
$$=(1+k+1)(k+1)!-1$$
$$=(k+2)!-1$$
Hence, by induction, the pattern holds for all \(k\geq1\).
24 December
Today's number is 191 more than one of the other answers and
100 less than another of the answers.