Advent calendar 2016
Advent 2016 murder mystery
2016's Advent calendar ended with a murder mystery, with each of
the murderer, motive, weapon and location being a digit from 1 to 9.
Here are the clues:
10
None of the digits of 171 is the location.
None of the digits of 171 is the location.
3
None of the digits of 798 is the motive.
None of the digits of 798 is the motive.
7
One of the digits of 691 is the location.
One of the digits of 691 is the location.
16
None of the digits of 543 is the location.
None of the digits of 543 is the location.
5
One of the digits of 414 is the murderer.
One of the digits of 414 is the murderer.
20
The first digit of 287 is the number of false red clues.
The first digit of 287 is the number of false red clues.
8
Clues on days that are factors of 768 are all true.
Clues on days that are factors of 768 are all true.
22
The murderer is the square root of one of the digits of 191.
The murderer is the square root of one of the digits of 191.
11
One of the digits of 811 is the weapon.
One of the digits of 811 is the weapon.
19
The highest common factor of the weapon and 128 is 1.
The highest common factor of the weapon and 128 is 1.
13
None of the digits of 512 is the murderer.
None of the digits of 512 is the murderer.
18
One of the digits of 799 is the motive.
One of the digits of 799 is the motive.
17
None of the digits of 179 is the motive.
None of the digits of 179 is the motive.
6
None of the digits of 819 is the location.
None of the digits of 819 is the location.
24
One of the digits of 319 is total number of false clues.
One of the digits of 319 is total number of false clues.
23
One of the digits of 771 is the murderer.
One of the digits of 771 is the murderer.
2
The weapon is not one of the digits of 435.
The weapon is not one of the digits of 435.
14
The final digit of 415 is the number of true blue clues.
The final digit of 415 is the number of true blue clues.
4
The weapon is a factor of 140.
The weapon is a factor of 140.
12
The number of false clues before today is the first digit of 419.
The number of false clues before today is the first digit of 419.
9
One of the digits of 447 is the motive.
One of the digits of 447 is the motive.
1
None of the digits of 563 is the motive.
None of the digits of 563 is the motive.
21
One of the digits of 816 is the murderer.
One of the digits of 816 is the murderer.
15
One of the digits of 387 is the motive.
One of the digits of 387 is the motive.
24 December
Today's number is 191 more than one of the other answers and
100 less than another of the answers.
23 December
Today's number is the number of three digit numbers that are not three more than a multiple of 7.
22 December
Today's number is a palindrome. Today's number is also the number of palindromes between 111 and 11111 (including 111 and 11111).
21 December
Today's number is a multiple of three. The average (mean) of all the answers that are multiples of three is a multiple of 193.
20 December
Earlier this year, I wrote a blog post about different ways to prove Pythagoras' theorem. Today's puzzle uses Pythagoras' theorem.
Start with a line of length 2. Draw a line of length 17 perpendicular to it. Connect the ends to make a right-angled triangle.
The length of the hypotenuse of this triangle will be a non-integer.
Draw a line of length 17 perpendicular to the hypotenuse and make another right-angled triangle. Again the new hypotenuse will have a non-integer length.
Repeat this until you get a hypotenuse of integer length. What is the length of this hypotenuse?
19 December
The sum of all the numbers in the eighth row of Pascal's triangle.
Clarification: I am starting the counting of rows from 1, not 0. So (1) is the 1st row, (1 1) is the 2nd row, (1 2 1) is the 3rd row, etc.
18 December
The smallest number whose sum of digits is 25.
17 December
The number of degrees in one internal angle of a regular polygon with 360 sides.
16 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number than can be made from the digits in red boxes.
| × | × | = 6 | |||
| × | × | × | |||
| × | × | = 180 | |||
| × | × | × | |||
| × | × | = 336 | |||
| = 32 | = 70 | = 162 |
15 December
A book has 386 pages. What do the page numbers on the two middle pages add up to?
14 December
In July, I posted the Combining Multiples puzzle.
Today's number is the largest number that cannot be written in the form \(27a+17b\), where \(a\) and \(b\) are positive integers (or 0).
13 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10. Today's number is the smaller number in a red box to the power of the larger number in a red box.
| + | - | = 8 | |||
| - | - | - | |||
| + | ÷ | = 3 | |||
| + | ÷ | × | |||
| + | × | = 120 | |||
| = 8 | = 1 | = 8 |
12 December
Here is a list of facts about today's number:
- If a×b is a factor of it, with a and b both positive integers, then either a or b is one.
- The sum of its digits is 14.
- It is odd.
- The product of its digits is 36.
- It is a palindrome when written in base 9.
- It is smaller than yesterday's number.
- It is 4 more than a multiple of 5.
- It is two less than a prime number.
- It is the number of a bus stopping at Richmond station.
11 December
This year, I have spend a lot of time working on the AVE game engine.
Today's answer is the code to the safe in this Christmas themed game.
10 December
The smallest number that is equal to the sum of its digits
multiplied by ten more than the sum of its digits.
9 December
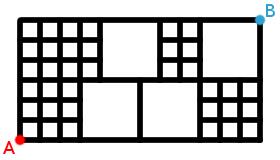
You start at A and are allowed to move either to the right or upwards.
How many different routes are there to get from A to B?
8 December
Today's number is the second smallest number that can be written as
a×b×c×d×e×f×g×h×i, where
a,b,...,i are all integers greater than 1.
7 December
Put the digits 1 to 9 (using each digit once) in the boxes so that the three digit numbers formed (reading left to right and top to bottom) have the desired properties written by their rows and columns.
| multiple of 25 | |||
| today's number | |||
| all digits even | |||
| multiple of 91 | multiple of 7 | cube number |
6 December
When you add up the digits of a number, the result is called the digital sum.
How many different digital sums do the numbers from 1 to 1091 have?*
* There was a mistake in this question (it previously said 1092).
If you answered the typo'd question right, your answer should automatically correct itself to 9 less than it was...
5 December
Today's number is the number of ways that 35 can be written as the sum of distinct numbers, with none of the numbers in the sum being divisible by 9.
Clarification: By "numbers", I mean (strictly) positive integers. The sum of the same numbers in a different order is counted as the same sum: eg. 1+34 and 34+1 are not different sums.
The trivial sum consisting of just the number 35 counts as a sum.
4 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10. Today's number is the product of the digits in the red boxes.
| + | ÷ | = 2 | |||
| + | ÷ | - | |||
| ÷ | - | = 5 | |||
| ÷ | - | × | |||
| - | × | = 4 | |||
| = 3 | = 5 | = 6 |
3 December
What is the volume of the smallest cube inside which a rectangular-based pyramid of volume 266 will fit?
2 December
What is the maximum number of lines that can be formed by the intersection
of 30 planes?
1 December
One of the digits of today's number was removed to leave a two digit number.
This two digit number was added to today's number.
The result was 619.