Puzzles
19 December
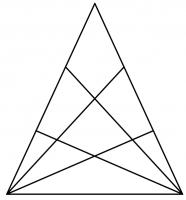
The diagram to the right shows a triangle. Two of the sides of the triangle have been split into three pieces, with lines drawn from the opposite vertex. In total, the diagram now contains 27 triangles of any size.
Another triangle has two of its sides split into eight pieces, with lines drawn from the opposite vertex. How many triangles (of any size) would this create?
Show answer
Hide answer
Each triangle must include one of the two corners at the base of the largest triangle (or both those corners).
To make triangles including the bottom left corner of the large triangle, we must pick two lines coming out of that corner, and one line coming out of the bottom right corner that is not the base of the triangle.
There are 9 lines coming out of the corners, so the total number of triangles is \(\left(\begin{array}{c}9\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=288\).
We now need to count the triangles that include the bottom right corner of the large triangle, but do not include both corners (as we've already counted thoses).
There are \(\left(\begin{array}{c}8\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=224\) ways to pick lines to make these triangles.
In total, this makes 512 triangles.
12 December
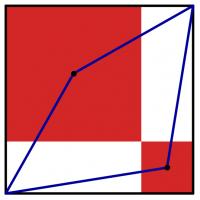
The diagram to the left shows a large black square. Inside this square, two red squares have been drawn.
(The sides of the red squares are parallel to the sides of the black square; each red square shares a vertex with the black square; and the two red squares share a vertex.)
A blue quadrilateral has then been drawn with vertices at two corners of the black square and the centres of the red squares.
The area of the blue quadrilateral is 167. What is the area of the black square?
Show answer
Hide answer
No matter the exact size of each square, the blue quadrilateral will always fill half the square, so the area of the square is 334.
2 December
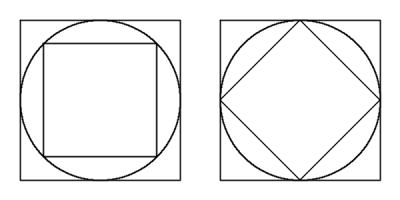
Carol draws a square with area 62. She then draws the smallest possible circle that this square is contained inside.
Next, she draws the smallest possible square that her circle is contained inside. What is the area of her second square?
Show answer
Hide answer
By drawing an appropriate diagram, it can be seen that the small square has half the area of the large square.
Therefore the area of the large square is 124.
19 December
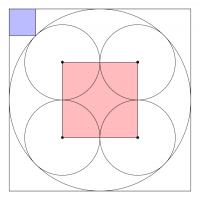
The diagram below shows three squares and five circles.
The four smaller circles are all the same size, and the red square's vertices are the centres of these circles.
The area of the blue square is 14 units. What is the area of the red square?
Show answer
Hide answer
The diagonal of the blue square is \(\sqrt{28}\). The radius \(R\) of the large circle satisfies \(R^2+R^2=(R+\sqrt{28})^2\).
Solving this, we find that \(R=\frac{\sqrt{28}}{\sqrt2-1}=\sqrt{28}(\sqrt2+1)\).
The radius \(r\) of the small circles satisfies \(r+r\sqrt2=R\), and so \(r=\frac{\sqrt{28}(\sqrt2+1)}{\sqrt2+1}=\sqrt{28}\).
The area of the square is \(4r^2=4\left(\sqrt{28}\right)^2=4\times28\). This is 112.
5 December
28 points are spaced equally around the circumference of a circle. There are 3276 ways to pick three of these points.
The three picked points can be connected to form a triangle. Today's number is the number of these triangles that are isosceles.
Show answer
Hide answer
Pick one of the 28 points and imagine a line to the point opposite it. There will be 13 points on each side of this line. Picking one of these 13 points and then picking the
corresponding point on the other side of the line gives an isosceles triangle. Therefore there are 13 isosceles triangles with the first chosen point as the point where the two equal sides meet.
There were 28 choices for the first point, and so the total number of isosceles triangles will be 13×28=364.
2 December
You have 15 sticks of length 1cm, 2cm, ..., 15cm (one of each length). How many triangles can you make by picking three sticks and joining their ends?
Note: Three sticks (eg 1, 2 and 3) lying on top of each other does not count as a triangle.
Note: Rotations and reflections are counted as the same triangle.
Show answer
Hide answer
In order to make a valid triangle, the sum of the two shorter sides must be larger than the longest side.
There is
1 triangle with longest side 4cm (2,3,4);
2 with longest side 5cm (2,4,5 and 3,4,5);
4 with longest side 6cm (2,5,6; 3,5,6; 4,5,6 and 3,4,6);
6 with longest side 7cm (2,6,7; 3,6,7; 4,6,7; 5,6,7; 3,5,7 and 4,5,7);
9 with longest side 8cm;
12 with longest side 9cm;
16 with longest side 10cm;
20 with longest side 11cm;
25 with longest side 12cm;
30 with longest side 13cm;
36 with longest side 14cm; and
42 with longest side 15cm.
In total this makes 203 triangles.
23 December
Today's number is the area of the largest area rectangle with perimeter 46 and whose sides are all integer length.
12 December
There are 2600 different ways to pick three vertices of a regular 26-sided shape. Sometimes the three vertices you pick form a right angled triangle.
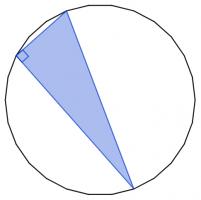
These three vertices form a right angled triangle.
Today's number is the number of different ways to pick three vertices of a regular 26-sided shape so that the three vertices make a right angled triangle.
Show answer
Hide answer
The vertices of the 26-gon lie on a circle. The triangle is therefore right-angled if (and only if) the longest side is a diameter of the circle.
In other words, the triangle is right angled if (and only if) two of its vertices are opposite vertices of the 26-gon.
There are 13 different pairs of opposite points on the 26-gon. For each of these, there are 24 remaining vertices that could be the third vertex of the triangle.
Therefore there are 13×24=312 different right angled triangles.
![](javascript:showlimage("advent2020triangles.png"))
![](javascript:showlimage("advent2020quads.png"))
![](javascript:showlimage("ad2020-ans-1.png"))
![](javascript:showlimage("advent2019circles.png"))
![](javascript:showlimage("advent2018-12.png"))