Puzzles
Ellipses
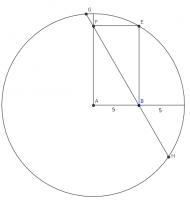
A piece of string 10cm long is tied to two pins 6cm apart.
The string is used to draw an ellipse. The pins are then moved 2cm further apart and a second ellipse is drawn. Which ellipse has the larger area?
Show answer & extension
Hide answer & extension
The area of an ellipse is \(\pi ab\) where \(a\) and \(b\) are the distances from the centre of the ellipse to the closest and furthest points on the ellipse.
In the first ellipse, \(a=5\mathrm{cm}\) and \(b=4\mathrm{cm}\), so the area is \(20\pi\mathrm{cm}^2\). In the second ellipse, \(a=5\mathrm{cm}\) and \(b=3\mathrm{cm}\), so the area is \(15\pi\mathrm{cm}^2\). Hence, the first ellipse has the larger area.
Extension
How far apart should the pins be placed to give the ellipse with the largest area?
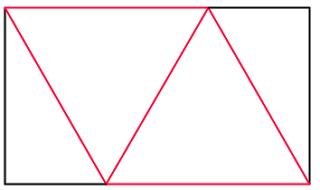
Folding tube maps
Back in 2012, I posted instructions for
folding a tetrahedron from tube maps. When tube maps are used, the sides of the tetrahedron are not quite equal. What ratio would the rectangular maps need to be in to give a regular tetrahedron?
Show answer & extension
Hide answer & extension
Once the map is folded, it will look like this:
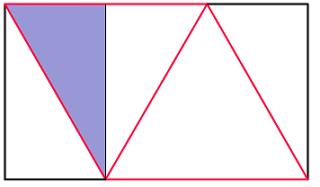
For the final tetrahedron to be regular, the red lengths must be equal. Let each red length be 2 (this will get rid of halves in the upcoming calculations). By drawing a vertical line in we can work out the width and height of the rectangle:
The width of the rectangle is 3 (one and a half red lengths). Using Pythagoras' Theorem in the blue triangle, we find that the height of the rectangle is \(\sqrt{3}\). Therefore, the ratio of the rectangle is \(\sqrt{3}:3\) or \(1:\sqrt{3}\).
Extension
If the ratio of the rectangle is \(1:a\), what is the ratio of the lengths of the sides of the tetrahedron?
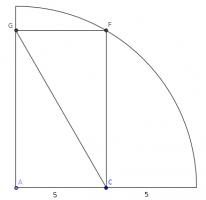
Circles
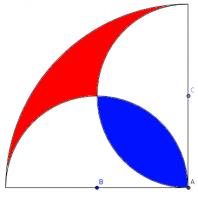
There is a quarter circle with radius 2r and centre A and two semi circles with radius r and centres B and C.
Prove that the red area is equal to the blue area.
Show answer & extension
Hide answer & extension
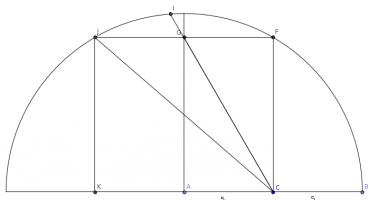
Call the blue area \(B\) and the red area \(R\).
$$R = \mbox{Area of quarter circle} - \mbox{Area of semicircle} - (\mbox{Area of semicircle} - B)$$
$$R = \frac{1}{4}\pi(2r)^2 - \frac{1}{2}\pi r^2 - \left(\frac{1}{2}\pi r^2 -B\right)$$
$$R = \pi r^2 - \frac{1}{2}\pi r^2 - \frac{1}{2}\pi r^2 +B$$
$$R=0+B$$
$$R=B$$
Extension
Prove that the red and blue areas are equal.
Pole position
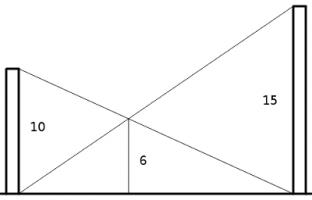
Two poles stand vertically on level ground. One is 10 feet tall, the other 15 feet tall. If a line is drawn from the top of each pole to the bottom of the other, the two lines intersect at a point 6 feet above the ground. What's the distance between the poles?
Show answer & extension
Hide answer & extension
The two poles can be any distance apart; the distance does not affect the heights.
Extension
If the heights of the two poles were 12m and 24m tall, what height would the intersection of the lines be?
If the heights of the two poles were \(a\)m and \(b\)m tall, what height would the intersection of the lines be?
![](javascript:showlimage("tetra1.png"))
![](javascript:showlimage("tetra2.png"))
![](javascript:showlimage("circle-diagonal.png"))
![](javascript:showlimage("circle-diagonal-extension.png"))
![](javascript:showlimage("circle-diagonal-extension2.png"))
![](javascript:showlimage("circles-puzzles-image.png"))
![](javascript:showlimage("extension.png"))
![](javascript:showlimage("2014-01-20-pole-position.png"))