Puzzles
Pole position
Source: Futility Closet
![](javascript:showlimage("2014-01-20-pole-position.png"))
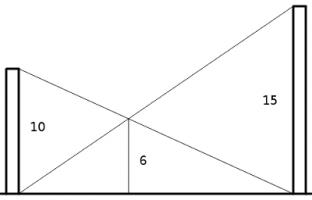
Two poles stand vertically on level ground. One is 10 feet tall, the other 15 feet tall. If a line is drawn from the top of each pole to the bottom of the other, the two lines intersect at a point 6 feet above the ground. What's the distance between the poles?
If you enjoyed this puzzle, check out Sunday Afternoon Maths I,
puzzles about geometry, or a random puzzle.
puzzles about geometry, or a random puzzle.