Puzzles
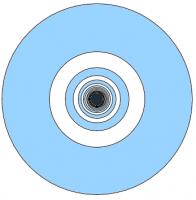
Dartboard
Concentric circles with radii 1, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), ... are drawn. Alternate donut-shaped regions are shaded.
What is the total shaded area?
Show answer & extension
Hide answer & extension
The shaded area is:
$$\pi (1)^2 - \pi (\frac{1}{2})^2 + \pi (\frac{1}{3})^2 - \pi (\frac{1}{4})^2 + \pi (\frac{1}{5})^2 - ...$$
$$=\sum_{i=1}^\infty \frac{\pi (-1)^{i-1}}{i^2}$$
$$=\pi\sum_{i=1}^\infty \frac{(-1)^{i-1}}{i^2}$$
$$=\pi\left(\frac{\pi^2}{12}\right)$$
$$=\frac{\pi^3}{12}$$
Extension
Prove that
$$=\sum_{i=1}^\infty \frac{(-1)^{i-1}}{i^2}=\frac{\pi^2}{12}$$
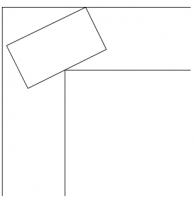
Grand piano
Jack and Jill are moving into a new flat and their grand piano presents a potential problem. Fortunately, it will just pass round the corridor without being tipped or disassembled.
Given that its area, looking down from above, is the largest possible which can be passed around the corner, what is the ratio of its length to its width?
Show answer & extension
Hide answer & extension
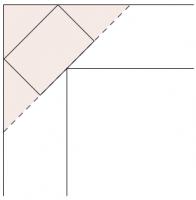
When halfway around the corner, the grand piano will look like this:
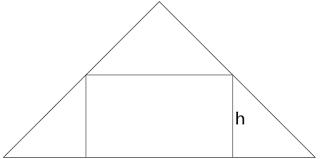
The problem then is finding the largest area rectangle which fits in the highlighted triangle: an isosceles triangle where the base is twice the height. Let the base be 2 and the height be 1.
If the height of the rectangle is \(h\), then its width is \(2(1-h)\). Therefore its area is \(2h-2h^2\). By differentiation, it can be seen that this is maximum when \(h=\frac{1}{2}\), which means that ratio of the rectangle's length to its width is 2:1.
Extension
If the corner was not a 90° angle, then what is the largest area rectangle which could fit round it?
Unit octagon
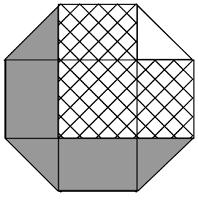
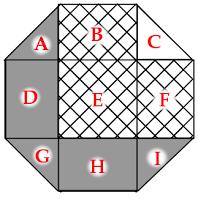
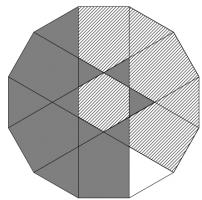
The diagram shows a regular octagon with sides of length 1. The octagon is divided into regions by four diagonals. What is the difference between the area of the hatched region and the area of the region shaded grey?
Show answer & extension
Hide answer & extension
Name the regions as follows:
\(E\) is a 1×1 square. Placed together, \(A\), \(C\), \(G\) and \(I\) also make a 1×1 square. \(B\) is equal to \(H\) and \(D\) is equal to \(F\).
Therefore \(B+E+F=A+C+D+G+H+I\). Therefore the hatched region is \(C\) larger than the shaded region. The area of \(C\) (and therefore the difference) is \(\frac{1}{4}\).
Extension
What is the difference between the shaded and the hatched regions in this dodecagon?
Largest triangle
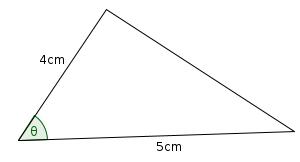
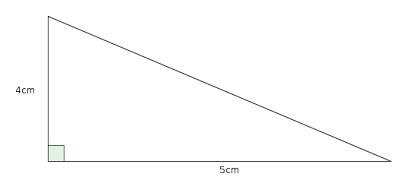
What is the largest area triangle which has one side of length 4cm and one of length 5cm?
Show answer & extension
Hide answer & extension
As our shape is a triangle, the 4cm and 5cm sides must be adjacent. Call the angle between them be \(\theta\).
The area of the triangle is \(\frac{1}{2}\times 4\times 5 \times \sin{\theta}\) or \(10\sin{\theta}\). This has a maximum value when \(\theta=90^\circ\), so the largest triangle has and area of 10cm2 and looks like:
Extension
What is the largest area triangle with a perimeter of 12cm?
Circles
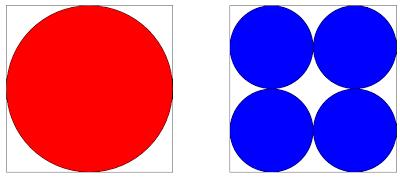
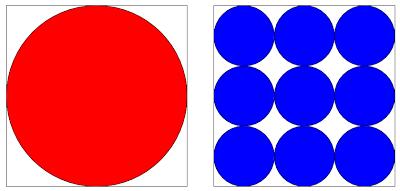
Which is largest, the red or the blue area?
Show answer & extension
Hide answer & extension
Let \(4x\) be the side length of the square. This means that the radius of the red circle is \(2x\) and the radius of a blue circle is \(x\). Therefore the area of the red circle is \(4\pi x^2\).
The area of one of the blue squares is \(\pi x^2\) so the blue area is \(4\pi x^2\). Therefore the two areas are the same.
Extension
Is the red or blue area larger?
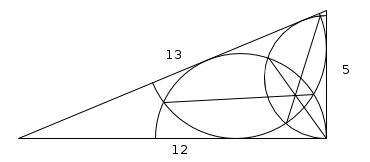
Semi circle in a triangle
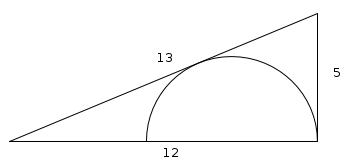
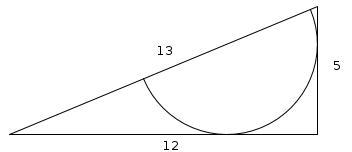
This right-angled triangle above has sides of lengths 12cm, 5cm and 13cm. The diameter of the semicircle lies on the 12cm side and the 13cm side is a tangent to the circle. What is the radius of the semi circle?
Show answer & extension
Hide answer & extension
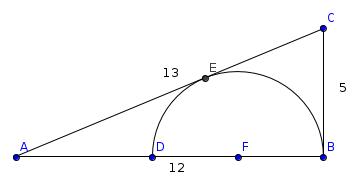
Label the triangle as follows:
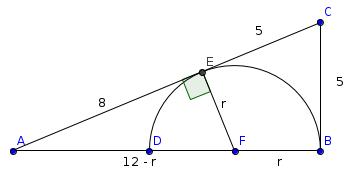
EC and BC are both tangents to the circle so FEA is a right angle and the lengths EC and BC are equal, so the length of EC is 5. Let r be the radius of the circle.
Using Pythagoras' Theorem in triangle FEA:
$$8^2+r^2=(12-r)^2$$
$$64+r^2=144-24r+r^2$$
$$24r=80$$
$$r=\frac{80}{24}=\frac{10}{3}$$
Extension
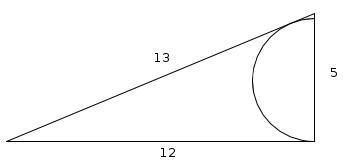
What is the radius of the circle whose diameter lies on the 5cm side and to which the 12cm and 13cm sides are tangents?
What is the radius of the circle whose diameter lies on the 13cm side and to which the 12cm and 5cm sides are tangents?
Additional observation
For each pair of semi circles, draw a straight line between the two points where the semi circles intersect. These lines all meet at a point.
Light work
"I don't know if you are fond of puzzles, or not. If you are, try this. ... A gentleman (a nobleman let us say, to make it more interesting) had a sitting-room with only one window in it—a square window, 3 feet high and 3 feet wide. Now he had weak eyes, and the window gave too much light, so (don't you like 'so' in a story?) he sent for the builder, and told him to alter it, so as only to give half the light. Only, he was to keep it square—he was to keep it 3 feet high—and he was to keep it 3 feet wide. How did he do it? Remember, he wasn't allowed to use curtains, or shutters, or coloured glass, or anything of that sort."
Equal areas
An equilateral triangle and a square have the same area. What is the ratio of the perimeter of the triangle to the perimeter of the square?
Show answer & extension
Hide answer & extension
Let \(A\) be the area of the square (and the triangle).
The length of a side of the square is \(\sqrt{A}\), so the perimeter of the square is \(4\sqrt{A}\).
Let \(l\) be the length of a side the triangle. Then \(\frac{1}{2}l^2\sin{60}=A\), so \(l^2=\frac{4A}{\sqrt{3}}\). Therefore \(l=\frac{2\sqrt{A}}{3^\frac{1}{4}}\) and the perimeter of the triangle is \(\frac{6\sqrt{A}}{3^\frac{1}{4}}\).
Hence the ratio of the perimeters is \(\frac{6\sqrt{A}}{3^\frac{1}{4}} : 4\sqrt{A}\) which simplifies to 33/4:2
Extension
If an \(n\) sided regular polygon has the area \(A\), what is the length of one of its sides?
![](javascript:showlimage("dartboard.png"))
![](javascript:showlimage("piano.png"))
![](javascript:showlimage("piano-ans.png"))
![](javascript:showlimage("piano-ans2.png"))
![](javascript:showlimage("octagon.png"))
![](javascript:showlimage("octagon-a1.png"))
![](javascript:showlimage("dodecagon.png"))
![](javascript:showlimage("triangle.png"))
![](javascript:showlimage("triangle-biggest.png"))
![](javascript:showlimage("circles.png"))
![](javascript:showlimage("circles-ext.png"))
![](javascript:showlimage("circle-and-triangle.png"))
![](javascript:showlimage("labelled-tricirc.png"))
![](javascript:showlimage("labelled-tricirc2.png"))
![](javascript:showlimage("ext1.png"))
![](javascript:showlimage("ext2.png"))
![](javascript:showlimage("ext3.png"))
