Puzzles
2 December
Holly adds up the first six even numbers, then adds on half of the next even number. Her total is 49.
Next, Holly adds up the first \(n\) even numbers then adds on half of the next even number. This time, her total is 465124. What is \(n\)?
1 December
Each interior angle of a regular triangle is 60°.
Each interior angle of a different regular polygon is 178°. How many sides does this polygon have?
Advent 2022 logic puzzle
It's nearly Christmas and something terrible has happened: an evil Christmas-hater has set three drones loose above Santa's stables. As long as the drones are flying around, Santa is unable to
take off to deliver presents to children all over the world.
You need to help Santa by destroying the drones so that he can deliver presents before Christmas is ruined for everyone.
Each of the three drones was programmed with four integers between 1 and 20 (inclusive): the first two of these are the drone's starting position; the last two give the drone's daily speed.
The drones have divided the sky above Santa's stables into a 20 by 20 grid. On 1 December, the drones will be at their starting position.
Each day, every drone will add the first number in their daily speed to their horizontal position, and the second
number to their vertical position. If the drone's position in either direction becomes greater than 20, the drone will subtract 20 from their position in that direction.
Midnight in Santa's special Advent timezone is at 5am GMT, and so the day will change and the drones will all move at 5am GMT.
For example, if a drone's starting position was (1, 12) and its movement was (5, 7), then:
- on day 1, it would be at (1, 12);
- on day 2, it would be at (6, 19);
- on day 3, it would be at (11, 6);
- on day 4, it would be at (16, 13);
- on day 5, it would be at (1, 20);
- on day 6, it would be at (6, 7);
- and so on.
You need to calculate each drone's starting position and daily speed, then work out where the drone currently is so you can shoot it down.
3
Blue's horizontal speed is not 3, 6, or 9.
14
On 4 December, blue's vertical position was 14.
15
Blue's vertical speed is not divisible by 2.
9
On 5 December, orange's vertical position was not 6.
2
Red's horizontal speed is a factor of 840.
6
Red's horizontal speed is not a factor of 128.
5
Blue's vertical speed is not 3, 1, or 5.
1
Red's vertical speed is 1.
12
Orange's horizontal speed is 1, 4, or 3.
24
The highest common factor of blue's horizontal speed and 28 is 1.
18
On 15 December, the horizontal position of one drone was 7.
8
Blue's vertical speed is a factor of 840.
11
Red's horizontal speed is 9, 8, or 7.
4
On 2 December, red's horizontal position was 5
16
Orange's horizontal speed is 3, 2, or 4.
22
Blue's horizontal speed is not a factor of 323.
10
On 8 December, the vertical position of two drones was 20.
19
On 16 December, the horizontal position of one drone was 8.
17
On 14 December, the horizontal position of one drone was 4.
21
Orange's horizontal speed is 2, 3, or 1.
13
On 6 December, the vertical position of two drones was 4.
20
Blue's horizontal speed is not 4, 2, or 5.
23
Blue's horizontal speed is 1 more or 1 less than a multiple of 5.
7
Blue's vertical speed is not 4, 7, or 6.
You can attempt to shoot down the drones here.
24 December
The expression \((3x-1)^2\) can be expanded to give \(9x^2-6x+1\). The
sum of the coefficients in this expansion is \(9-6+1=4\).
What is the sum of the coefficients in the expansion of \((3x-1)^7\)?
23 December
How many numbers are there between 100 and 1000 that contain no 0, 1, 2, 3, or 4?
22 December
Ivy makes a sequence by starting with the number 35, then repeatedly making the next term by reversing the digits of the current number and adding 6.
The first few terms of this sequence are:
$$35$$
$$53+6 = 59$$
$$95+6 = 101$$
What is the first number in Ivy's sequence that is smaller than the previous term?
21 December
In the annual tournament of Christmas puzzles, each player must play one puzzle match
against each other player. Last year there were four entrants into the tournament (A, B, C, and D),
and so 6 matches were played: A vs B, C vs D, A vs D, A vs C, D vs B, and finally B vs C.
This year, the tournament has grown in popularity and 22 players have entered. How many
matches will be played this year?
20 December
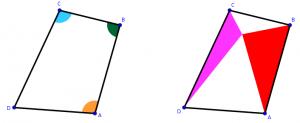
The diagram to the right shows (two copies of) quadrilateral ABCD.
The sum of the angles ABC and BCD (green and blue in quadrilateral on the left) is 180°.
The sum of the angles ABC and DAB (green and orange in quadrilateral on the left) is also 180°.
In the diagram on the right, a point inside the quadrilateral has been used to draw two triangles.
The area of the quadrilateral is 850. What is the smallest that the total area of the two triangles
could be?