Puzzles

445 in base 10 is equal to 544 in base 7.

Find another pair of bases \(A\) and \(B\) so that there exist digits \(d\), \(e\) and \(f\) such that \(def\) in base \(A\) is equal to \(fed\) in base \(B\)?

a+(a+A)^-1 = a + A = 2.

So, a+2^-1 = 2

So, a = ³/₂

By the same method, b = 2-√2, c = -2 and d = 2-2^k

For which values of k does this converge?

If \(ab\) in base 10 is equal to \(ba\) in base 4, then \(10a+b=4b+a\).

So, \(9a=3b\).

\(a\) and \(b\) must both be less than 4, as they are digits used in base 4, so \(a=1\) and \(b=3\).

So 13 in base 10 is equal to 31 in base 4.

By the same method, we find that:

For which pairs of bases \(A\) and \(B\) can you find two digits \(g\) and \(h\) such that \(gh\) in base \(A\) is equal to \(hg\) in base \(B\)?

Every item bought will cause the pence in the total cost to fall by 1. So to spend £65.76, Susanna must have bought 24 items.

What is the smallest amount Susanna could spend for which we could not tell how many items she bought?

\(T_{n} = \frac{1}{2}n(n+1)\), so:

So, we are looking for \(n\) such that \((n+1)^2+(n+3)^2=(n+5)^2\). This is true when \(n=5\) (\(6^2+8^2=10^2\)).

Find \(n\) such that \(T_{n}+T_{n+1}+T_{n+1}+T_{n+2}=T_{n+2}+T_{n+3}\).

The area of an ellipse is \(\pi ab\) where \(a\) and \(b\) are the distances from the centre of the ellipse to the closest and furthest points on the ellipse.

In the first ellipse, \(a=5\mathrm{cm}\) and \(b=4\mathrm{cm}\), so the area is \(20\pi\mathrm{cm}^2\). In the second ellipse, \(a=5\mathrm{cm}\) and \(b=3\mathrm{cm}\), so the area is \(15\pi\mathrm{cm}^2\). Hence, the first ellipse has the larger area.

How far apart should the pins be placed to give the ellipse with the largest area?

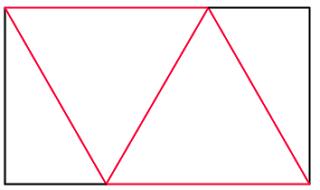
Once the map is folded, it will look like this:

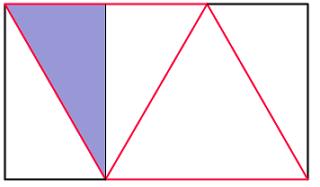
For the final tetrahedron to be regular, the red lengths must be equal. Let each red length be 2 (this will get rid of halves in the upcoming calculations). By drawing a vertical line in we can work out the width and height of the rectangle:

The width of the rectangle is 3 (one and a half red lengths). Using Pythagoras' Theorem in the blue triangle, we find that the height of the rectangle is \(\sqrt{3}\). Therefore, the ratio of the rectangle is \(\sqrt{3}:3\) or \(1:\sqrt{3}\).

If the ratio of the rectangle is \(1:a\), what is the ratio of the lengths of the sides of the tetrahedron?

\(y=x^{x^{x^{x^{...}}}}\) so \(y=x^y=e^{y\ln{x}}\).

By the chain and product rules, \(\frac{dy}{dx}=e^{y\ln{x}}(\frac{dy}{dx}\ln{x}+\frac{y}{x})\).

Rearranging, we get \(\frac{dy}{dx}=\frac{ye^{y\ln{x}}}{x(1-e^{y\ln{x}}\ln{x})}\).

This simplifies to \(\frac{dy}{dx}=\frac{x^{x^{x^{x^{...}}}}x^{x^{x^{x^{...}}}}}{x(1-x^{x^{x^{x^{...}}}}\ln{x})}\).

What would the graph of \(y=x^{x^{x^{x^{...}}}}\) look like?