Puzzles
Three digit numbers
Brigette wrote down a list of all 3-digit numbers. For each of the numbers on her list she found the product of the digits. She then added up all of these products. Which of the following is equal to her total?
A \(45\)
B \(45^2\)
C \(45^3\)
D \(2^{45}\)
E \(3^{45}\)
Show answer & extension
Hide answer & extension
The sum of the products is:
$$\sum_{i=1}^{9}\sum_{j=1}^{9}\sum_{k=1}^{9}ijk$$
$$=(\sum_{i=1}^{9}i)(\sum_{j=1}^{9}j)(\sum_{k=1}^{9}k)$$
$$=45\times45\times45$$
$$=45^3$$
Extension
Find the sum of the products of the digits of all n digit numbers.
Multiple sums
If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.
Find the sum of all the multiples of 3 or 5 below 1000.
Show answer & extension
Hide answer & extension
The multiples of 3 less than 1000 are 3,6,9,...,999; the multiples of 5 are 5,10,15,...,995. Multiples of 15 (15,30,...,990) will appear in both lists so we are trying to find (3+6+9+...+999)+(5+10+15+...+995)-(15+30+...+990). This is:
$$\sum_{i=1}^{333}3i+\sum_{j=1}^{199}5j-\sum_{k=1}^{66}15k$$
$$=3\sum_{i=1}^{333}i+5\sum_{j=1}^{199}j-15\sum_{k=1}^{66}k$$
$$=3\times\frac{333\times334}{2}+5\times\frac{199\times200}{2}-15\times\frac{66\times67}{2}$$
$$=166833+99500-33165$$
$$=233168$$
Extension
Find the sum of all the multiples of 3 or 5 below \(n\).
Downing Street
A knot of spectators in Downing Street was watching members of the Cabinet as they arrived for a critical meeting.
"Who's that?" I asked my neighbour, as a silk-hatted figure, carrying rolled umbrella, rang the bell at No. 10. "Is it the Minister of Maths?"
"Yes," he said.
"Quite right," said a second spectator. "The Minister of Maths it is. Looks grim, doesn't he?"
The first of the speakers tells the truth three times out of four. The second tells the truth four times out of five.
What is the probability that the gentleman in question was in fact the Minister of Maths?
Show answer & extension
Hide answer & extension
The probabilities can be summarised as follows:
| First person truthful | First person lying |
| Second person truthful | \(\frac{3}{4}\times\frac{4}{5}=\frac{12}{20}\) | \(\frac{1}{4}\times\frac{4}{5}=\frac{4}{20}\) |
| Second person lying | \(\frac{3}{4}\times\frac{1}{5}=\frac{3}{20}\) | \(\frac{1}{4}\times\frac{1}{5}=\frac{1}{20}\) |
As they both agree, only both lying and both truthful are possible. Hence the chance of them lying is 1/13 and the chance of them telling the truth, and it indeed being the Minister of Maths, is 12/13
Extension
If the first person said it was the Minister of English and the second said it was the Minister of Maths, what is the probability that it was the Minister of Maths?
Chessboard squares
It was once claimed that there are 204 squares on a chessboard. Can you justify this claim?
Show answer & extension
Hide answer & extension
There are 64 1×1 squares, 49 2×2 squares, 36 3×3 squares, 25 4×4 squares, 16 5×5 squares, 9 6×6 squares, 4 7×7 squares and 1 8×8 square on a chessboard.
This can be shown by counting how many positions the top left corner of the square can sit on. For example, the top left corner of a 5×5 square can be in the first four rows and columns of the board (otherwise the square will go off the board) and 4×4=16.
64+49+36+25+16+9+4+1=204.
Extension
How many rectangles are there on a chessboard?
Equal areas
An equilateral triangle and a square have the same area. What is the ratio of the perimeter of the triangle to the perimeter of the square?
Show answer & extension
Hide answer & extension
Let \(A\) be the area of the square (and the triangle).
The length of a side of the square is \(\sqrt{A}\), so the perimeter of the square is \(4\sqrt{A}\).
Let \(l\) be the length of a side the triangle. Then \(\frac{1}{2}l^2\sin{60}=A\), so \(l^2=\frac{4A}{\sqrt{3}}\). Therefore \(l=\frac{2\sqrt{A}}{3^\frac{1}{4}}\) and the perimeter of the triangle is \(\frac{6\sqrt{A}}{3^\frac{1}{4}}\).
Hence the ratio of the perimeters is \(\frac{6\sqrt{A}}{3^\frac{1}{4}} : 4\sqrt{A}\) which simplifies to 33/4:2
Extension
If an \(n\) sided regular polygon has the area \(A\), what is the length of one of its sides?
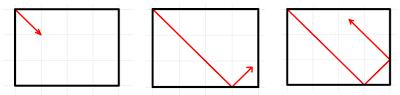
Rebounds
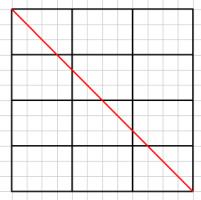
In a 4x3 rectangle, a ball is fired from the top left corner at 45°.
It bounces around a rectangle until it hits a corner. Which corner does it end in?
Which corner will it end in for rectangles of other sizes?
Show answer & extension
Hide answer & extension
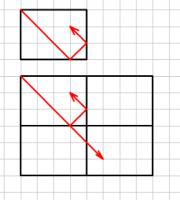
If mirrors were placed along the walls of the rectangle, the ball would appear to travel in a straight line across a grid of rectangles:
Viewed this way, the ball will still stop once it reaches a corner:
For an \(n\) by \(m\) (in above example: \(n=4\), \(m=3\)) rectangle, this will occur once the ball has travelled through \(\mathrm{lcm}(n,m)\) squares.
$$\mathrm{Let\ }a=\frac{\mathrm{lcm}(n,m)}{n}$$
$$\mathrm{Let\ }b=\frac{\mathrm{lcm}(n,m)}{m}$$
On its way to the corner, the ball will bounce \(b-1\) times off the top and bottom and \(a-1\) times off the sides. It can be seen that if \(a-1\) is even, then the ball will end in one of the corners on the right hand side. The complete results can be seen in the following
Carroll diagram:
| \(a-1\) odd | \(a-1\) even |
| \(b-1\) odd | Top left | Top right |
| \(b-1\) even | Bottom left | Bottom right |
It can be shown that the ball will never finish in the top left (where it started) as this would require it to travel through the bottom right first. Therefore the following holds:
| \(a\) even | \(a\) odd |
| \(b\) even | | Top right |
| \(b\) odd | Bottom left | Bottom right |
Extension
For which sizes of rectangle will the path of the ball make the same pattern?
Complex squares
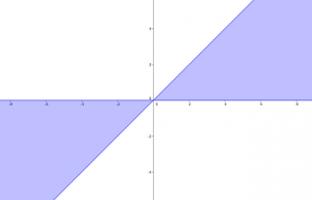
For which complex numbers, \(z\), are \(\mathrm{Re}(z^2)\) and \(\mathrm{Im}(z^2)\) both positive?
Show answer & extension
Hide answer & extension
Any complex number can be written in the form \(z=re^{i\theta}\).
This gives that \(z^2=r^2e^{2i\theta}\), which will have positive real and complex parts when \(0+2\pi n < 2\theta < \frac{\pi}{2}+2\pi n\).
This will occur when \(0 < \theta < \frac{\pi}{4}\) and \(\pi < \theta < \frac{5\pi}{4}\).
A complex number \(z\) falls in these regions when \(|\mathrm{Re}(z)|>|\mathrm{Im}(z)|\) and \(\mathrm{sign}(\mathrm{Re}(z))=\mathrm{sign}(\mathrm{Im}(z))\).
Extension
For which complex numbers, \(z\), are \(\mathrm{Re}(z^3)\) and \(\mathrm{Re}(z^3)\) both positive?
Adding bases
Let \(a_b\) denote \(a\) in base \(b\).
Find bases \(A\), \(B\) and \(C\) less than 10 such that \(12_A+34_B=56_C\).