Puzzles
No change
"Give me change for a dollar, please," said the customer.
"I'm sorry," said the cashier, "but I can't do it with the coins I have. In fact, I can't change a half dollar, quarter, dime or nickel."
"Do you have any coins at all?" asked the customer.
"Oh yes," said the cashier, "I have $1.15 in coins."
Which coins are in the cash register?
(The available coins are 50¢, 25¢, 10¢ 5¢ and 1¢.)
Dirty work
Timothy, Urban, and Vincent are digging identical holes in a field.
When Timothy and Urban work together, they dig 1 hole in 4 days.
When Timothy and Vincent work together, they dig 1 hole in 3 days.
When Urban and Vincent work together, they dig 1 hole in 2 days.
Working alone, how long does it take Timothy to dig one hole?
Show answer & extension
Hide answer & extension
Let \(t\), \(u\) and \(v\) be the prortion of a hole dug in one day by Timothy, Urban and Vincent respectively. Then the following equations hold:
$$4t+4u=1$$$$3t+3v=1$$$$2u+2v=1$$
These can be solved to find that \(t=\frac{1}{24}\) so it will take Timothy 24 days to dig a hole.
Extension
Working alone, how long does it take Urban to dig one hole?
Working alone, how long does it take Vincent to dig one hole?
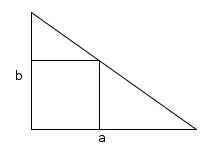
Square in a triangle
A right-angled triangle has short sides of length \(a\) and \(b\). A square is drawn in the triangle so that two sides lie on the sides of the triangle and a corner lies on the hypotenuse.
What is the length of a side of the square?
Show answer & extension
Hide answer & extension
Call the length of a side of the square \(x\). CAB and CEF are similar triangles, therefore:
$$\frac{EF}{AB}=\frac{EC}{AC}$$
$$\frac{x}{a}=\frac{b-x}{b}$$
$$bx=ab-ax$$
$$x=\frac{ab}{a+b}$$
Extension
Consider a tetrahedron with vertices at \((0,0,0)\), \((a,0,0)\), \((0,b,0)\) and \((0,0,c)\). A cube is placed in the tetrahedron so that three of its faces are in the xy, xz and yz planes and one of its vertices lies on the other face.
What is the length of a side of the cube?
Double derivative
What is
$$\frac{d}{dy}\left(\frac{dy}{dx}\right)$$
when:
(i) \(y=x\)
(ii) \(y=x^2\)
(iii) \(y=x^3\)
(iv) \(y=x^n\)
(v) \(y=e^x\)
(vi) \(y=\sin(x)\)?
Show answer & extension
Hide answer & extension
(ii) Differentiating \(y=x^2\) with respect to \(x\) \(\frac{dy}{dx}=2x\). Let \(g=\frac{dy}{dx}\). By the chain rule:
$$\frac{dg}{dy}=\frac{dg}{dx}\frac{dx}{dy}$$
$$=2\frac{1}{2x}$$
$$=\frac{1}{x}$$
So \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=\frac{1}{x}\)
(iii) By the same method, \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=\frac{2}{x}\)
(iv) \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=\frac{n-1}{x}\)
(v) \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=1\)
(vi) \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=-\tan(x)\)
Extension
What is
$$\frac{d}{dy}\left(\frac{dy}{dx}\right)$$
when \(y=f(x)\)?
Equal opportunity
Can two (six-sided) dice be weighted so that the probability of each of the numbers 2, 3, ..., 12 is the same?
Show answer & extension
Hide answer & extension
Let \(p_1\), \(p_2\), ..., \(p_6\) be the probabilities of getting 1 to 6 on one die and \(q_1\), ..., \(q_6\) on the other. The probability of getting a total of 2 is \(p_1q_1\) and the probabilty of getting a total of 12 is \(p_6q_6\). Therefore \(p_1q_1=p_6q_6\).
If \(p_1\geq p_6\) then \(q_1\leq q_6\) (and vice-versa) as otherwise the above equality could not hole. Therefore:
$$(p_1-p_6)(q_1-q_6)\leq 0$$
$$p_1q_1-p_6q_1-p_1q_6+p_6q_6\leq 0$$
$$p_1q_1+q_6p_6\leq p_1q_6+p_6q_1$$
The probability of rolling a total of 7 is \(p_1q_6+p_2q_5+...+p_6q_1\). This is larger than \(p_1q_6+p_6q_1\), which is larger than (or equal to) \(p_1q_1+q_6p_6\), which is larger than \(p_1q_1\).
Therefore the probability of rolling a 7 is larger than the probability of rolling a two, so it is not possible.
Extension
Can two \(n\)-sided dice be weighted so that the probability of each of the numbers 2, 3, ..., 2\(n\) is the same?
Can a \(n\)-sided die and a \(m\)-sided die be weighted so that the probability of each of the numbers 2, 3, ..., \(n+m\) is the same?
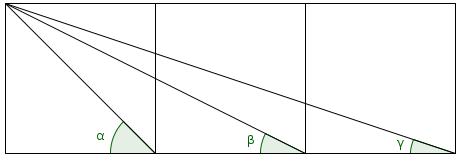
Three squares
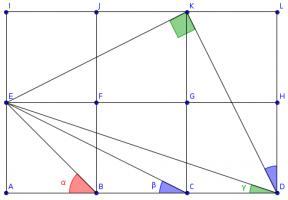
The diagram shows three squares with diagonals drawn on and three angles labelled.
What is the value of \(\alpha+\beta+\gamma\)?
Show answer & extension
Hide answer & extension
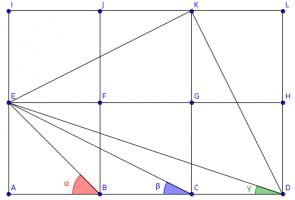
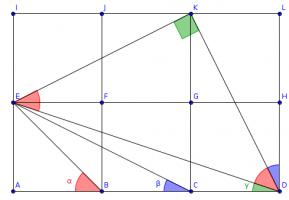
Draw three more squares and add these lines (I have coloured the angles to make equal angles clearer):
Triangles \(ACE\), \(LDK\) and \(IKE\) are congruent, so angle \(KDL\) is equal to \(\beta\).
The congruence of these triangles tells us that angles \(DKL\) and \(EKI\) add up to a right angle, so angle \(EKD\) is also a right angle.
The congruence of the triangles also tells us that \(KD\) and \(KE\) are the same length and so angle \(EDK\) is the angle in an isosceles right-angled triangle. \(\alpha\) is also the angle in an isosceles right-angled triangle, so these two angles are equal.
Therefore \(\alpha+\beta+\gamma=90^\circ\).
Extension
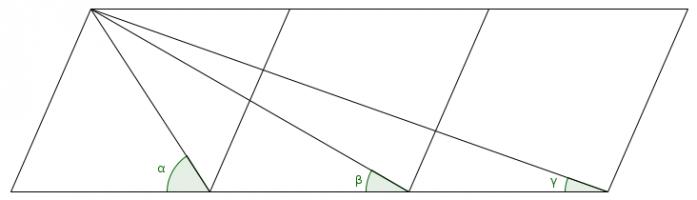
The diagram shows three rhombuses with diagonals drawn on and three angles labelled.
What is the value of \(\alpha+\beta+\gamma\)?
The ace of spades
I have three packs of playing cards with identical backs. Call the packs A, B and C.
I draw a random card from pack A and shuffle it into pack B.
I now turn up the top card of pack A, revealing the Queen of Hearts.
Next, I draw a card at random from pack B and shuffle it into pack C. Then, I turn up the top card of pack B, revealing another Queen of Hearts.
I now draw a random card from pack C and place it at the bottom of pack A.
What is the probability that the card at the top of pack C is the Ace of Spades?
Show answer
Hide answer
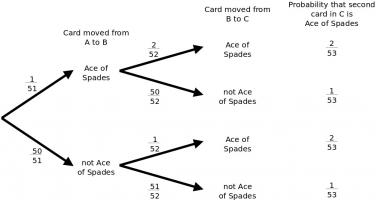
The problem can be expressed using the following probability tree:
The probability that the card turned over from C is an Ace of Spades is:
$$\frac{1\times 2\times 2+1\times 50\times 1+50\times 1\times 2+50\times 51\times 1}{51\times 52\times 53}$$
$$=\frac{52}{51\times 53}$$
3n+1
Let \(S=\{3n+1:n\in\mathbb{N}\}\) be the set of numbers one more than a multiple of three.
(i) Show that \(S\) is closed under multiplication.
ie. Show that if \(a,b\in S\) then \(a\times b\in S\).
Let \(p\in S\) be irreducible if \(p\not=1\) and the only factors of \(p\) in \(S\) are \(1\) and \(p\). (This is equivalent to the most commonly given definition of prime.)
(ii) Can each number in \(S\) be uniquely factorised into irreducibles?
Show answer & extension
Hide answer & extension
(i) Let \(a,b\in S\). Then \(\exists \alpha,\beta\in \mathbb{N}\) such that \(a=3\alpha+1\) and \(b=3\beta+1\).
(This says that if \(a\) and \(b\) are in \(S\) then they can be written as a multiple of three plus one.)
$$a\times b=(3\alpha+1)\times (3\beta+1)$$
$$=9\alpha\beta+3\alpha+3\beta+1$$
$$=3(3\alpha\beta+\alpha+\beta)+1$$
This is a multiple of three plus one, so \(a\times b\in S\).
(ii) No, as \(36\times 22=4\times 253\) and 36,22,4 and 253 are all irreducible.
Extension
Try the task again with \(S=\{a+b\sqrt{2}:a,b\in\mathbb{Z}\}\).
![](javascript:showlimage("sq-in-tri.png"))
![](javascript:showlimage("three-squares.png"))
![](javascript:showlimage("three-ans1.png"))
![](javascript:showlimage("three-ans2.png"))
![](javascript:showlimage("three-ans3.png"))
![](javascript:showlimage("three-ans4.png"))
![](javascript:showlimage("three-rhombus.png"))
![](javascript:showlimage("prob-tree.jpg"))