Puzzles
17 December
If you expand \((a+b+c)^2\), you get \(a^2+b^2+c^2+2ab+2ac+2bc\).
This has 6 terms.
How many terms does the expansion of \((a+b+c+d+e+f)^5\) have?
16 December
Some numbers can be written as the sum of two or more consecutive positive integers, for example:
$$7=3+4$$
$$18=5+6+7$$
Some numbers (for example 4) cannot be written as the sum of two or more consecutive positive integers.
What is the smallest three-digit number that cannot be written as the sum of two or more consecutive positive integers?
Show answer & extension
Hide answer & extension
Every number except the powers of 2 can be written as the sum of two or more consecutive positive integers. The smallest
three-digit power of 2 is 128.
Extension
Why can every number that isn't a power of 2 be written as the sum of two or more consecutive positive integers?
15 December
The arithmetic mean of a set of \(n\) numbers is computed by adding up all the numbers, then
dividing the result by \(n\).
The geometric mean of a set of \(n\) numbers is computed by multiplying all the numbers together, then
taking the \(n\)th root of the result.
The arithmetic mean of the digits of the number 132 is \(\tfrac13(1+3+2)=2\).
The geometric mean of the digits of the number 139 is \(\sqrt[3]{1\times3\times9}\)=3.
What is the smallest three-digit number whose first digit is 4 and for which the arithmetic and geometric means of its digits are both non-zero integers?
Show answer & extension
Hide answer & extension
The only three digit number whose first digits is 4 and for which the arithmetic and geometric means of its digits are both non-zero integers is 444.
Extension
How many three digit numbers are there for which the arithmetic and geometric means of its digits are both non-zero integers?
How many four digit numbers are there for which the arithmetic and geometric means of its digits are both non-zero integers?
14 December
The function \(f(x)=ax+b\) (where \(a\) and \(b\) are real constants) satisfies
$$-x^3+2x^2+6x-9\leqslant f(x)\leqslant x^2-2x+3$$
whenever \(0\leqslant x\leqslant3\). What is \(f(200)\)?
Show answer
Hide answer
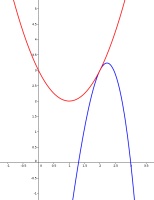
How to get started with this puzzle is easiest to see if we plot the two curves:
We see that the two curves meet at the point (2,3). The only way that the straight line \(f\) can be between the two curves is if it is a tangent to both curves.
By differentiation of another way of finding tangents, you can show that \(a=2\) and \(b=1\). Therefore \(f(200)\) is 399.
13 December
Today's number is given in this crossnumber. No number in the completed grid starts with 0.
|
|
| Across |
| 1 | Today's number. | (3) |
| 4 | A multiple of 5 times the sum of the digits of 2D. | (3) |
| 5 | Greater than two times 3D. | (3) |
|
| Down |
| 1 | The sum of 5A and 3D. | (3) |
| 2 | Nine times the sum of the digits of 4A. | (3) |
| 3 | Greater than 2D. | (3) |
|
Show answer
Hide answer
2D is a multiple of 9, and so its digits add up to a multiple of 9. This means that 4A is a multiple of 9, and its digits add up to a multiple of 9 too.
The digits of 4A can add up to at most 27 (if it's 999) and so must add add up to 9, 18, or 27. These would make 2D equal to 81, 162, or 243 respectively. 2D cannot be 81 (as it's a three-digit number);
it also can't be 243, as this would mean 4A was 999, leading to a clash in the centre square. Therefore the sum of the digits of 4A is 18 and 2D is 162:
The sum of the digits of 4A is 18, so 4A is 369, 468, 567, 666, 765, 864, or 963. Of these, only 765 is a multiple of 5, and so 4A must be 765:
3D is greater than 2D, so the first digit of 3D is at least 2. If the first digit of 3D was 3 or higher, then 5A would be greater than 700, meaning 1D would be greater than 1000 and not a three-digit number.
Therefore:
The last digits of 3D and 5A are the same, and so the last digit of 1D (and the first digit of 5A) must be even. 5A is greater than 500, and so it's first digit must be 6 or 8;
it cannot be 8 as this would make 1D greater than 100. And so:
This only leaves one option for the last two digits to make 1D's clue correct:
Today's number is 812.
12 December
What is the smallest value of \(n\) such that
$$\frac{500!\times499!\times498!\times\dots\times1!}{n!}$$
is a square number?
Show answer
Hide answer
Consider the first two terms in the product:
$$
500!\times499!
=500\times499!\times499!$$
$$= 500\times(499!)^2.$$
Doing similar steps with each pair of terms in the product, we see that:
$$
500!\times499!\times498!\times\dots\times1!
=
500\times498\times\dots\times2\times(499!\times497!\times\dots\times1!)^2
$$
$$
=
(2\times250)\times(2\times249)\times\dots\times(2\times1)\times(499!\times497!\times\dots\times1!)^2
$$
$$
=
2^{250}\times250!\times(499!\times497!\times\dots\times1!)^2
$$
If we divide this by \(250!\), we are left with a square number, and so \(n\) is 250
11 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | + | | = 15 |
| + | | + | | ÷ | |
| + | | – | | = 10 |
| + | | – | | × | |
| ÷ | | × | | = 3 |
=
16 | | =
1 | | =
30 | |
Show answer
Hide answer
| 3 | + | 7 | + | 5 | = 15 |
| + | | + | | ÷ | |
| 9 | + | 2 | – | 1 | = 10 |
| + | | – | | × | |
| 4 | ÷ | 8 | × | 6 | = 3 |
=
16 | | =
1 | | =
30 | |
The product of the numbers in the red boxes is 120.
10 December
How many integers are there between 100 and 1000 whose digits add up to an even number?
Show answer
Hide answer
Between 100 and 109 (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number.
Between 110 and 119 (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number...
In general, between \(10n\) and \(10n+9\) (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number.
The integers from 100 to 999 (inclusive) can be split into 45 sets of integers from \(10n\) to \(10n+9\) (and the digits of 1000 don't add to an even number), so there are
450 integers between 100 and 1000 whose digits add up to an even number.