Puzzles
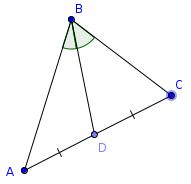
Two triangles
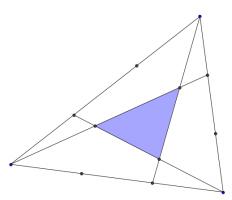
The three sides of this triangle have been split into three equal parts and three lines have been added.
What is the area of the smaller blue triangle as a fraction of the area of the original large triangle?
Show answer & extension
Hide answer & extension
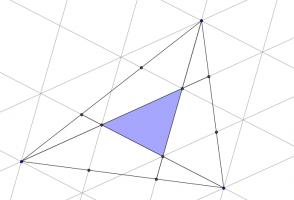
Draw on the following lines parallel to those which were added in the question.
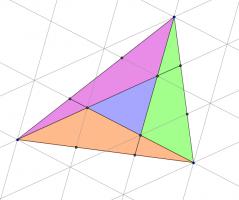
Then a grid of copies of the smaller blue triangle has been created. Now consider the three triangles which are coloured green, purple and orange in the following diagram:
Each of these traingles covers half a parallelogram made from four blue triangles. Therefore the area of each of these triangles is twice the area of the small blue triangle.
And so the blue triangle covers one seventh of the large triangle.
Extension
If the sides of the triangle were split into \(n\) pieces the the lines added, what would the area of the smaller blue triangle be as a fraction of the area of the original large triangle?
Dodexagon
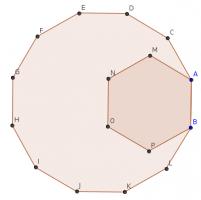
In the diagram, B, A, C, D, E, F, G, H, I, J, K and L are the vertices of a regular dodecagon and B, A, M, N, O and P are the vertices of a regular hexagon.
Show that A, M and E lie on a straight line.
Show answer & extension
Hide answer & extension
The interior angle of a regular hexagon is 120°. The interior angle of a regular dodecagon is 150°. Therefore angle CAM is 30°.
Now, consider the quadrilateral ACDE. This quadrilateral is symmetric (as the dodecagon is regular) so the angles CAE and DEA are equal. Hence:
$$360 = CAE+DEA+ACD+CDE\\
= 2CAE + 2\times 150\\
2CAE = 60\\
CAE=30
$$
The angles CAM and CAE are equal, so A, M and E lie on a straight line.
Extension
The vertices \(P_1\), \(P_2\), ..., \(P_n\) make up a regular \(n\)-gon and \(Q_1\), \(Q_2\), ..., \(Q_m\) make up a regular \(m\)-gon, with \(P_1=Q_1\) and \(P_2=Q_2\).
The vertices \(P_2\), \(Q_3\) and \(P_5\) lie on a straight line. What is the relationship between \(m\) and \(n\)?
Products and sums of squares
Show that the product of any two numbers, each of which is the sum of two square integers, is itself the sum of two square integers.
Show answer & extension
Hide answer & extension
The result of the multiplication can be written as:
$$(a^2+b^2)(c^2+d^2)$$
where \(a\), \(b\), \(c\) and \(d\) are integers. Expanding the brackets gives:
$$a^2c^2+b^2c^2+a^2d^2+b^2d^2$$
Next, if \((bd-ac)^2\) and \((bc+ad)^2\) are expanded, we get:
$$(bd-ac)^2=b^2d^2+a^2c^2-2abcd$$
$$(bc+ad)^2=b^2c^2+a^2d^2+2abcd$$
And so:
$$(a^2+b^2)(c^2+d^2)=(bd-ac)^2+(bc+ad)^2$$
We have written the product as the sum of two integers.
Extension
For which integers \(a\), \(b\), \(c\) and \(d\) can the result \((a^2+b^2)(c^2+d^2)\) be written as the sum of two square integers in more than one way?
Equal side and angle
In the diagram shown, the lengths \(AD = CD\) and the angles \(ABD=CBD\).
Prove that the lengths \(AB=BC\).
Show answer
Hide answer
By the sine rule in BCD:
$$\frac{CD}{\sin(CBD)}=\frac{BD}{\sin(BCD)}$$
By the sine rule in BAD:
$$\frac{AD}{\sin(ABD)}=\frac{BD}{\sin(BAD)}$$
\(ABD=CBD\) and \(AD=CD\), so:
$$\sin(BAD)=\frac{BD\sin(ABD)}{AD}\\
=\frac{BD\sin(CBD)}{CD}\\
=\sin(BCD)$$
Using the sine rule in ABC:
$$\frac{AB}{\sin(BCD)}=\frac{BC}{\sin(BAD)}$$
The two sines are equal and so:
$$AB=BC$$
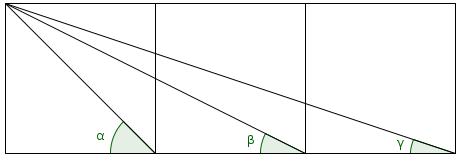
Arctan
Prove that \(\arctan(1)+\arctan(2)+\arctan(3)=\pi\).
Show answer & extension
Hide answer & extension
Let \(\alpha=\arctan(1)\), \(\beta=\arctan(2)\) and \(\gamma=\arctan(3)\), then draw the angles as follows:
Extension
Can you find any other integers \(a\), \(b\) and \(c\) such that:
$$\arctan(a)+\arctan(b)+\arctan(c)=\pi$$
A bit of Spanish
Each of the letters P, O, C, M, U and H represent a different digit from 0 to 9.
Which digit does each letter represent?
Show answer & extension
Hide answer & extension
POCO is 4595 and MUCHO is 68925.
Extension
The question could be written as \(POCO\times 15=MUCHO\).
For which values of \(n\) are the letters uniquely defined by \(POCO\times n = MUCHO\)?
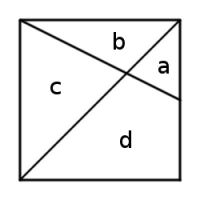
Square deal
This unit square is divided into four regions by a diagonal and a line that connects a vertex to the midpoint of an opposite side. What are the areas of the four regions?
Show answer & extension
Hide answer & extension
The square is unit, so \(a+b+c+d=1\). By the definitions of the lines, \(a+d=\frac{1}{2}\) and \(a+b=\frac{1}{4}\).
\(a\) and \(c\) are similar triangles. The vertical side of \(c\) is twice that of \(a\) so \(c=4a\).
Therefore we have the system of simultaneous equations:
$$a+b+c+d=1\\a+d=\frac{1}{2}\\a+b=\frac{1}{4}\\c=4a$$
These can be solved to find:
$$a=\frac{1}{12}\\b=\frac{1}{6}\\c=\frac{1}{3}\\d=\frac{5}{12}\\$$
Extension
What would be the areas if the lines were a diagonal and another line which divides the sides in the ratio \(x:y\)?
Odd squares
Prove that 1 and 9 are the only square numbers where all the digits are odd.
Show answer & extension
Hide answer & extension
If \(n^2\) has all odd digits then the units digit of \(n\) must be odd. It can be checked that \(n\) cannot be a one digit number (except 1 or 3 as given in the question) as the tens digit will be even.
Therefore \(n\) can be written as \(10A+B\) where \(A\) is a positive integer and \(B\) is an odd positive integer.
$$n^2=(10A+B)^2\\=100A+20AB+B^2$$
Now consider the tens digit of this.
\(100A\) has no effect on this digit. The tens digit of \(20AB\) will be the units digit of \(2AB\) which will be even. The tens digit of \(B^2\) is even (as checked above). Therefore the tens digit of \(n^2\) is even.
Hence 1 and 9 are the only square numbers where all the digits are odd.
Extension
For which bases is this not true?
![](javascript:showlimage("two triangles.png"))
![](javascript:showlimage("two-tri-ans1.png"))
![](javascript:showlimage("two-tri-ans2.png"))
![](javascript:showlimage("dodexagon.png"))
![](javascript:showlimage("equal-side-and-angle.png"))
![](javascript:showlimage("three-squares.png"))
![](javascript:showlimage("spanish.png"))
![](javascript:showlimage("square-deal.png"))