Puzzles
Make the sums
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, \(4+3\times2\) is 14, not 10.
| + | | - | | = 4 |
| + | | - | | × | |
| - | | × | | = 27 |
| - | | × | | ÷ | |
| × | | ÷ | | = 16 |
=
2 | | =
8 | | =
6 | |
Show answer & extension
Hide answer & extension
| 1 | + | 5 | - | 2 | = 4 |
| + | | - | | × | |
| 7 | - | 4 | × | 9 | = 27 |
| - | | × | | × | |
| 6 | × | 8 | - | 3 | = 16 |
=
2 | | =
8 | | =
6 | |
Extension
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct.
| + | | - | | = 5 |
| - | | - | | - | |
| + | | ÷ | | = 5 |
| + | | ÷ | | × | |
| + | | × | | = 99 |
=
0 | | =
1 | | =
18 | |
Rotating round table
At a large dinner, 24 people are to sit evenly spaced around a round table. Place cards are laid to show where everyone should sit. Unfortunately nobody notices the name cards and the guests sit down with nobody in the correct seat.
Show that it is possible to rotate the table so that at least two people will be in the correct seats.
Show answer & extension
Hide answer & extension
Let \(p(n)\) denote the number of people in the correct seat when the table is rotated by \(n\) people. From the question, we know that:
$$p(0)=0$$
As every guest can be put into the correct place by one rotation, we know that:
$$p(0)+p(1)+...+p(23)=24$$
As \(p(0)=0\):
$$p(1)+...+p(23)=24$$
This sum has 23 positive integers adding up to 24, so one of the rotations must lead to at least two people being in the correct places.
Extension
If the 24 guests sat randomly and one person was in the correct seat, could you still rotate the table so that two people are correctly seated?
Balanced sets
A set of points in the plane is called 'balanced' if for any two points \(A\) and \(B\) in the set, there is another point \(C\) in the set such that \(AC=BC\) (here \(AC\) is the distance between \(A\) and \(C\)).
For all \(n\geq3\), find a balanced set of \(n\) points.
Show answer
Hide answer
If \(n\) is odd, the vertices of a regular \(n\)-gon are balanced.
If \(n\) is even, a balanced set can be constructed as follows:
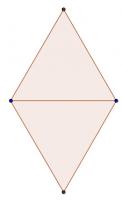
If \(n=4\), this set is balanced (both the triangles are equilateral):
Draw a triangle with its centre at one of the points, going through the other three points:
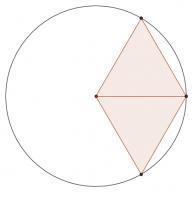
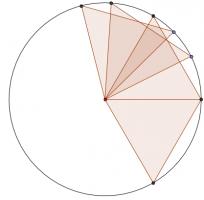
For \(n>4\), repeatedly add a two new points on the circle which form an equilateral triangle with the centre. For example, for \(n=6\), this set is balanced:
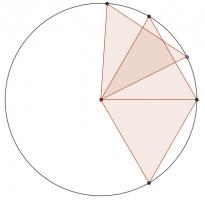
And for \(n=8\), this set is balanced:
121
Find a number base other than 10 in which 121 is a perfect square.
Ticking clock
Is there a time of day when the hands of an analogue clock (one with a second hand that moves every second instead of moving continuously) will all be 120° apart?
Show answer & extension
Hide answer & extension
The second hand will always be pointing at one of the 60 graduations. If the minute and hour hand are 120° away from the second hand they must also be pointing at one of the graduations. The minute hand will only be pointing at a graduation at zero seconds past the minute, so the second hand must be pointing at 0. Therefore the hand are either pointing at: hour: 4, minute: 8, second: 0; or hour: 8, minute: 4, second: 0. Neither of these are real times, so it is not possible
Extension
If the second hand moves continuously instead of moving every second, will there be a time when the hands of the clock are all 120° apart?
One two three
Each point on a straight line is either red or blue. Show that it's always possible to find three points of the same color in which one is the midpoint of the other two.
Show answer & extension
Hide answer & extension
Pick two points (A and B) of the same colour (say red). Consider the points:
- C such that B is the midpoint of AC.
- D such that A is the midpoint of BD.
- E such that E is the midpoint of AB.
If at least one of C, D or E is red, then three equally spaced red points have been found. If C, D and E are blue, then they are three equally spaced blue points.
Extension
Will there be four equally spaced points of the same colour?
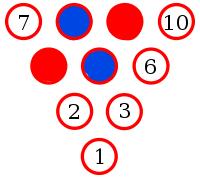
Coloured pins
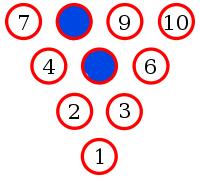
A bowling alley has a mixture of red and blue pins. Ten of these pins are randomly chosen and arranged in a triangle.
Will there always be three pins of the same colour which lie on the vertices of an equilateral triangle?
Show answer & extension
Hide answer & extension
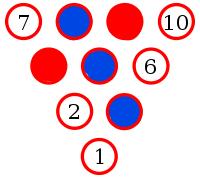
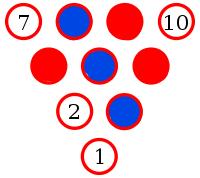
Yes. To show this, let's suppose there is an arrangement of pins with no monochrome triangle.
Let the middle pin be blue (if it is not blue, then swapping all the colours will make it blue without adding/removing monochrome triangles).
Pins 8, 2 and 6 make a triangle. Therefore one of these pins must be blue. By symmetry, any of these situations is equivalent to 8 being blue.
Pins 9 and 4 must be red to prevent a blue triangle.
Pin 3 must be blue to prevent a red triangle.
Pin 6 must be red to prevent a blue triangle.
But now whichever colour 10 is, it will make a monochrome triangle. Therefore there must be three pins of the same colour which lie on the vertices of an equilateral triangle.
Extension
What is the smallest \(n\) such that any mixture of \(n^2\) red and blue pins arranged in a square grid must contain four pins of the same colour which lie on the vertices of a square?
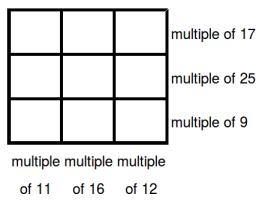
Fill in the digits
Can you place the digits 1 to 9 in the boxes so that the three digit numbers formed in the top, middle and bottom rows are multiples of 17, 25 and 9 (respectively); and the three digit numbers in the left, middle and right columns are multiples of 11, 16 and 12 (respectively)?