Puzzles
The taxman
In a very strange country, the tax system works as follows.
£1, £2, £3 up to £12 are available.
You pick an amount. You keep this amount, but the taxman takes any factors of it. You cannot pick any amount without a factor.
This continues until you can take no more money. The taxman gets any remaining money.
For example, you might play as follows:
- Take £12. Taxman gets £1, £2, £3, £4, £6.
- Take £10. Taxman gets £5.
- You cannot take anything. Taxman gets £7, £8, £9, £11.
In this example, you end with £22 and the taxman ends with
£56.
Is it possible to get more money than the taxman? What is the most you can get?
Show answer & extension
Hide answer & extension
The maximum you can get is £50, with the taxman getting
£28. Here is
how to get it:
- Take £11. Taxman gets £1.
- Take £9. Taxman gets £3.
- Take £8. Taxman gets £2, £4.
- Take £10. Taxman gets £5.
- Take £12. Taxman gets £6.
- You cannot take anything. Taxman gets £7.
Extension
Can you always beat the taxman if £1 up to £\(n\) are
available?
Squared circle
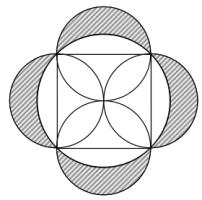
Each side of a square has a circle drawn on it as diameter. The square is also inscribed in a fifth circle as shown.
Find the ratio of the total area of the shaded crescents to the area
of the square.
Show answer
Hide answer
Let the radius of the small circles be \(r\). The are of half of one of these circles is \(\frac{1}{2}\pi r^2\).
The side of the square is \(2r\) and so the area of the square is \(4r^2\). Therefore the area of the whole shape is \((4+2\pi)r^2\).
By Pythagoras' Theorem, the radius of the large circle is \(r\sqrt{2}\). Therefore the area of the circle is \(2\pi r^2\). This means that the shaded area is \((4+2\pi)r^2 - 2\pi r^2\) or \(4r^2\).
This is the same as the area of the square, so the ratio is 1:1.
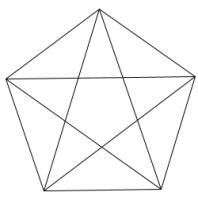
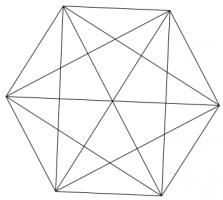
Polygraph
Draw a regular polygon. Connect all its vertices to every other vertex. For example, if you picked a pentagon or a hexagon, the result would look as follows:
Colour the regions of your shape so that no two regions which share an edge are the same colour. (Regions which only meet at one point can be the same colour.)
What is the least number of colours which this can be done with?
Show answer & extension
Hide answer & extension
It can be done with two colours. Let's call these red and blue.
Draw the polygon and colour it red. As each line is added to is, swap the colours on one side of the line which leaving them the same on the other side. At the end of this process you will have any polygon coloured with two colours.
Extension
How many regions will the regular shape be split into by the lines?
The sixth cent
You toss 6 fair coins, and I toss 5 fair coins. What is the probability that you get more heads than I do?
Show answer & extension
Hide answer & extension
As You have one more coin than me, if you don't throw more heads than me, then you must throw more tails than me.
This means that the probability of you throwing more heads then me plus the probability of you throwing more tails then me is equal to one.
By symmetry, the probabilities for heads and tails must be equal and so the probability that you throw more heads is \(\frac{1}{2}\)
Extension
You toss \(n\) fair coins, and I toss \(m\) fair coins. What is the probability that you get more heads than I do?
One hundred factorial
How many zeros does \(100!\) end with?
Show answer & extension
Hide answer & extension
The number of zeros at the end of a number is the same as the number of 10s in the product that makes the number. Each of these 10s is made by multiplying 5 by 2.
There will be more even numbers than multiples of 5 in \(100!\), so the number of 5s will tell us how many zeros the number ends in.
In \(100!\), there will be 20 multiples of 5 and 4 multiples of \(5^2\). This means that \(100!\) will end in 24 zeros.
Extension
How many zeros will \(n!\) end in?
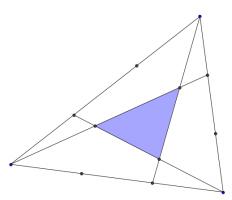
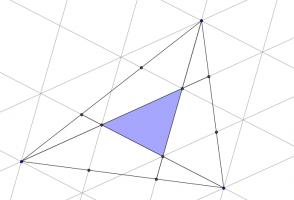
Two triangles
The three sides of this triangle have been split into three equal parts and three lines have been added.
What is the area of the smaller blue triangle as a fraction of the area of the original large triangle?
Show answer & extension
Hide answer & extension
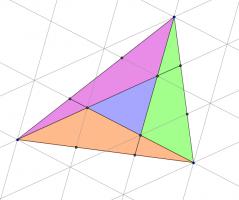
Draw on the following lines parallel to those which were added in the question.
Then a grid of copies of the smaller blue triangle has been created. Now consider the three triangles which are coloured green, purple and orange in the following diagram:
Each of these traingles covers half a parallelogram made from four blue triangles. Therefore the area of each of these triangles is twice the area of the small blue triangle.
And so the blue triangle covers one seventh of the large triangle.
Extension
If the sides of the triangle were split into \(n\) pieces the the lines added, what would the area of the smaller blue triangle be as a fraction of the area of the original large triangle?
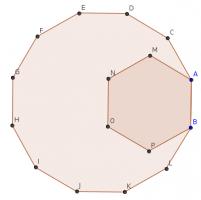
Dodexagon
In the diagram, B, A, C, D, E, F, G, H, I, J, K and L are the vertices of a regular dodecagon and B, A, M, N, O and P are the vertices of a regular hexagon.
Show that A, M and E lie on a straight line.
Show answer & extension
Hide answer & extension
The interior angle of a regular hexagon is 120°. The interior angle of a regular dodecagon is 150°. Therefore angle CAM is 30°.
Now, consider the quadrilateral ACDE. This quadrilateral is symmetric (as the dodecagon is regular) so the angles CAE and DEA are equal. Hence:
$$360 = CAE+DEA+ACD+CDE\\
= 2CAE + 2\times 150\\
2CAE = 60\\
CAE=30
$$
The angles CAM and CAE are equal, so A, M and E lie on a straight line.
Extension
The vertices \(P_1\), \(P_2\), ..., \(P_n\) make up a regular \(n\)-gon and \(Q_1\), \(Q_2\), ..., \(Q_m\) make up a regular \(m\)-gon, with \(P_1=Q_1\) and \(P_2=Q_2\).
The vertices \(P_2\), \(Q_3\) and \(P_5\) lie on a straight line. What is the relationship between \(m\) and \(n\)?
Products and sums of squares
Show that the product of any two numbers, each of which is the sum of two square integers, is itself the sum of two square integers.
Show answer & extension
Hide answer & extension
The result of the multiplication can be written as:
$$(a^2+b^2)(c^2+d^2)$$
where \(a\), \(b\), \(c\) and \(d\) are integers. Expanding the brackets gives:
$$a^2c^2+b^2c^2+a^2d^2+b^2d^2$$
Next, if \((bd-ac)^2\) and \((bc+ad)^2\) are expanded, we get:
$$(bd-ac)^2=b^2d^2+a^2c^2-2abcd$$
$$(bc+ad)^2=b^2c^2+a^2d^2+2abcd$$
And so:
$$(a^2+b^2)(c^2+d^2)=(bd-ac)^2+(bc+ad)^2$$
We have written the product as the sum of two integers.
Extension
For which integers \(a\), \(b\), \(c\) and \(d\) can the result \((a^2+b^2)(c^2+d^2)\) be written as the sum of two square integers in more than one way?