Puzzles
6 December
\(p(x)\) is a quadratic with real coefficients. For all real numbers \(x\),
$$x^2+4x+14\leq p(x)\leq 2x^2+8x+18$$
\(p(2)=34\). What is \(p(6)\)?
5 December
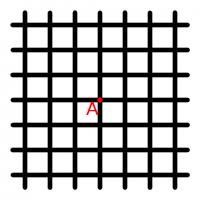
You start at A and are allow to walk left, right, up or down along the grid. The grid continues forever in every direction. After you have walked thirteen units, how many different locations could you be in?
4 December
Pick a three digit number whose digits are all different.
Sort the digits into ascending and descending order to form two new numbers. Find the difference between these numbers.
Repeat this process until the number stops changing. The final result is today's number.
3 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10. Today's number is the product of the numbers in the red boxes.
| + | + | = 17 | |||
| + | ÷ | × | |||
| ÷ | - | = 1 | |||
| - | × | ÷ | |||
| ÷ | - | = 0 | |||
| = 4 | = 12 | = 27 |
2 December
There are three cards; one number is written on each card. You are told that the sums of pairs of cards are 99, 83 and 102.
What is the sum of all three cards?
1 December
Today's number is the smallest three digit number such that the sum of its digits is equal to the product of its digits.
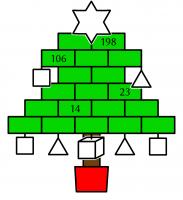
What's the star?
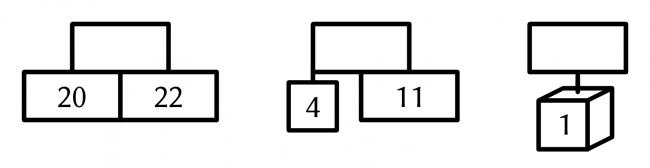
In the Christmas tree below, the rectangle, baubles, and the star at the top each contain a number. The square baubles contain square numbers; the triangle baubles contain triangle numbers; and the cube bauble contains a cube number.
The numbers in the rectangles (and the star) are equal to the sum of the numbers below them. For example, if the following numbers are filled in:
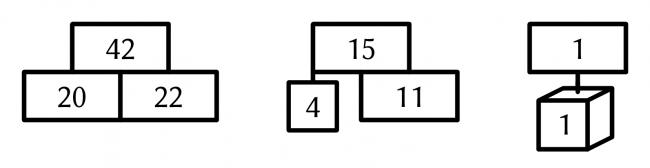
then you can deduce the following:
What is the number in the star at the top of this tree?
You can download a printable pdf of this puzzle here.
XYZ
Source: Futility Closet
Which digits \(X\), \(Y\) and \(Z\) fill this sum?
$$
\begin{array}{cccc}
&X&Z&Y\\
+&X&Y&Z\\
\hline
&Y&Z&X
\end{array}
$$