Puzzles
Is it equilateral?
Source: Chalkdust issue 07
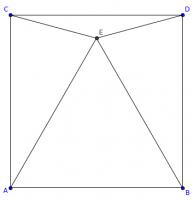
In the diagram below, \(ABDC\) is a square. Angles \(ACE\) and \(BDE\) are both 75°.
Is triangle \(ABE\) equilateral? Why/why not?
Cube multiples
Source: Radio 4's Puzzle for Today (set by Daniel Griller)
Six different (strictly) positive integers are written on the faces of a cube. The sum of the numbers on any two adjacent faces is a multiple of 6.
What is the smallest possible sum of the six numbers?
Advent 2017 logic puzzle
2017's Advent calendar ended with a logic puzzle: It's nearly Christmas and something terrible has happened: Santa and his two elves have been cursed! The curse has led Santa to forget which present three children—Alex, Ben and Carol—want and where they live.
The elves can still remember everything about Alex, Ben and Carol, but the curse is causing them to lie. One of the elves will lie on even numbered days and tell the truth on odd numbered days; the other elf will lie on odd numbered days and tell the truth on even numbered days. As is common in elf culture, each elf wears the same coloured clothes every day.
Each child lives in a different place and wants a different present. (But a present may be equal to a home.) The homes and presents are each represented by a number from 1 to 9.
Here are the clues:
21
White shirt says: "Yesterday's elf lied: Carol wants 4, 9 or 6."
White shirt says: "Yesterday's elf lied: Carol wants 4, 9 or 6."
10
Orange hat says: "249 is my favourite number."
Orange hat says: "249 is my favourite number."
5
Red shoes says: "Alex lives at 1, 9 or 6."
Red shoes says: "Alex lives at 1, 9 or 6."
16
Blue shoes says: "I'm the same elf as yesterday. Ben wants 5, 7 or 0."
Blue shoes says: "I'm the same elf as yesterday. Ben wants 5, 7 or 0."
23
Red shoes says: "Carol wants a factor of 120. I am yesterday's elf."
Red shoes says: "Carol wants a factor of 120. I am yesterday's elf."
4
Blue shoes says: "495 is my favourite number."
Blue shoes says: "495 is my favourite number."
15
Blue shoes says: "Carol lives at 9, 6 or 8."
Blue shoes says: "Carol lives at 9, 6 or 8."
22
Purple trousers says: "Carol wants a factor of 294."
Purple trousers says: "Carol wants a factor of 294."
11
White shirt says: "497 is my favourite number."
White shirt says: "497 is my favourite number."
6
Pink shirt says: "Ben does not live at the last digit of 106."
Pink shirt says: "Ben does not live at the last digit of 106."
9
Blue shoes says: "Ben lives at 5, 1 or 2."
Blue shoes says: "Ben lives at 5, 1 or 2."
20
Orange hat says: "Carol wants the first digit of 233."
Orange hat says: "Carol wants the first digit of 233."
1
Red shoes says: "Alex wants 1, 2 or 3."
Red shoes says: "Alex wants 1, 2 or 3."
24
Green hat says: "The product of the six final presents and homes is 960."
Green hat says: "The product of the six final presents and homes is 960."
17
Grey trousers says: "Alex wants the first digit of 194."
Grey trousers says: "Alex wants the first digit of 194."
14
Pink shirt says: "One child lives at the first digit of 819."
Pink shirt says: "One child lives at the first digit of 819."
3
White shirt says: "Alex lives at 2, 1 or 6."
White shirt says: "Alex lives at 2, 1 or 6."
18
Green hat says: "Ben wants 1, 5 or 4."
Green hat says: "Ben wants 1, 5 or 4."
7
Green hat says: "Ben lives at 3, 4 or 3."
Green hat says: "Ben lives at 3, 4 or 3."
12
Grey trousers says: "Alex lives at 3, 1 or 5."
Grey trousers says: "Alex lives at 3, 1 or 5."
19
Purple trousers says: "Carol lives at 2, 6 or 8."
Purple trousers says: "Carol lives at 2, 6 or 8."
8
Red shoes says: "The digits of 529 are the toys the children want."
Red shoes says: "The digits of 529 are the toys the children want."
13
Green hat says: "One child lives at the first digit of 755."
Green hat says: "One child lives at the first digit of 755."
2
Red shoes says: "Alex wants 1, 4 or 2."
Red shoes says: "Alex wants 1, 4 or 2."
24 December
Today's number is the smallest number with exactly 28 factors (including 1 and the number itself as factors).
23 December
In the song The Twelve Days of Christmas, how many presents have been given after 8 days?
22 December
22 is two times an odd number. Today's number is the mean of all the answers on days (including today) that are two times an odd number.
Clarification: You are taking the mean for answers on days that are two times an odd numbers; ie. the days are two times odd, not the answers.
21 December
The factors of 6 (excluding 6 itself) are 1, 2 and 3. \(1+2+3=6\), so 6 is a perfect number.
Today's number is the only three digit perfect number.
20 December
What is the largest number that cannot be written in the form \(10a+27b\), where \(a\) and \(b\) are nonnegative integers (ie \(a\) and \(b\) can be 0, 1, 2, 3, ...)?