Puzzles
12 December
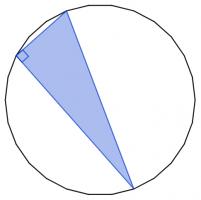
There are 2600 different ways to pick three vertices of a regular 26-sided shape. Sometimes the three vertices you pick form a right angled triangle.
Today's number is the number of different ways to pick three vertices of a regular 26-sided shape so that the three vertices make a right angled triangle.
11 December

This puzzle is inspired by a puzzle Woody showed me at MathsJam.
Today's number is the number \(n\) such that $$\frac{216!\times215!\times214!\times...\times1!}{n!}$$ is a square number.
10 December
The equation \(x^2+1512x+414720=0\) has two integer solutions.
Today's number is the number of (positive or negative) integers \(b\) such that \(x^2+bx+414720=0\) has two integer solutions.
9 December
Today's number is the number of numbers between 10 and 1,000 that contain no 0, 1, 2 or 3.
8 December
Arrange the digits 1-9 in a 3×3 square so: each digit the first row is the number of letters in the (English) name of the previous digit, each digit in the second row is one less than the previous digit, each digit in the third row is a multiple of the previous digit; the second column is an 3-digit even number, and the third column contains one even digit.
The number in the first column is today's number.
| each digit is the number of letters in the previous digit | |||
| each digit is one less than previous | |||
| each digit is multiple of previous | |||
| today's number | even | 1 even digit |
Edit: There was a mistake in this puzzle: the original had two solutions. If you entered the wrong solution, it will automatically change to the correct one.
7 December
There is a row of 1000 closed lockers numbered from 1 to 1000 (inclusive). Near the lockers, there is a bucket containing the numbers 1 to 1000 (inclusive) written on scraps of paper.
1000 people then each do the following:
- Pick a number from the bucket (and don't put it back).
- Walk along the row of lockers and change the state (open them if they're closed and close them if they're open) of all the lockers that are multiples of the number they picked (including the number they picked).
Today's number is the number of lockers that will be closed at the end of this process.
6 December

This puzzle is inspired by a puzzle that Daniel Griller showed me.
Write down the numbers from 12 to 22 (including 12 and 22). Under each number, write down its largest odd factor*.
Today's number is the sum of all these odd factors.
* If a number is odd, then its largest odd factor is the number itself.
5 December
I make a book by taking 111 sheets of paper, folding them all in half, then stapling them all together through the fold.
I then number the pages from 1 to 444.
Today's number is the sum of the two page numbers on the centre spread of my book.