Advent calendar 2024
21 December
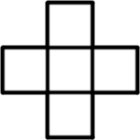
Noel wants to write a different non-zero digit in each of the five boxes below so that
the products of the digits of the three-digit numbers reading across and down are the same.
What is the smallest three-digit number that Noel could write in the boxes going across?