Puzzles
4 December
Today's number is a three digit number which is equal to the sum of the cubes of its digits. One less than today's number also has this property.
Show answer
Hide answer
If the final digit of the number is 0, then some carrying takes place when 1 is subtracted. Otherwise, no carrying happens.
If no carrying happens, call the three digits of today's number \(A\), \(B\), and \(C\). We know that \(A^3+B^3+C^3\) is one more than \(A^3 + B^3 + (C-1)^3\).
This implies that \(C^3=(C-1)^3+1\), which is only possible if \(C\) is 1.
Therefore either the final digit of today's number is 0 or the final digt of one less that today's number is 0. In both cases, we need to find a number
with the desired property whose final digit is 0: we are looking for digit \(A\) and \(B\) such that \(A^3+B^3\) is a multiple of 10.
Looking at all the cube numbers, there are a few combinations that add up to multiple of 10:
$$0^3+0^3=0$$
$$1^3+9^3=730$$
$$2^3+8^3=520$$
$$3^3+7^3=370$$
$$4^3+6^3=280$$
$$5^3+5^3=250$$
The only one of these that has the required property is 370. By checking 369 and finding it doesn't have the property, we see that the two numbers must be
370 and 371.
3 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number you can make with the digits in the red boxes.
| ÷ | | - | | = 3 |
| + | | + | | ÷ | |
| ÷ | | × | | = 1 |
| × | | - | | + | |
| - | | × | | = 20 |
=
91 | | =
6 | | =
8 | |
Show answer
Hide answer
| 9 | ÷ | 1 | - | 6 | = 3 |
| + | | + | | ÷ | |
| 4 | ÷ | 8 | × | 2 | = 1 |
| × | | - | | + | |
| 7 | - | 3 | × | 5 | = 20 |
=
91 | | =
6 | | =
8 | |
The largest number you can make with the digits in the red boxes is 321.
2 December
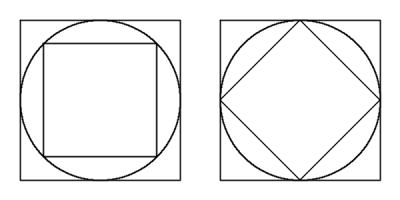
Carol draws a square with area 62. She then draws the smallest possible circle that this square is contained inside.
Next, she draws the smallest possible square that her circle is contained inside. What is the area of her second square?
Show answer
Hide answer
By drawing an appropriate diagram, it can be seen that the small square has half the area of the large square.
Therefore the area of the large square is 124.
1 December
It is possible to write 325 different numbers using the digits 1, 2, 3, 4, and 5 at most once each (and using no other digits).
How many of these numbers are odd?
Show answer
Hide answer
There are 3 one-digit numbers using these digits (1, 3 and 5).
To make two-digit odd numbers, there are 3 choices for the units digit, and 4 remaining choices for the tens digit.
To make three-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, and 3 remaining choices for the hundreds digit.
To make four-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, 3 remaining choices for the hundreds digit, and 2 remaining choices for the thousands digit.
To make five-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, 3 remaining choices for the hundreds digit, 2 remaining choices for the thousands digit and 1 remaining choice for the ten-thousands digit.
In total, this gives 3 + 3×4× + 3×4×3 + 3×4×3×2 + 3×4×3×2×1 = 195 odd numbers.
24 December
There are six 3-digit numbers with the property that the sum of their digits is equal to the product of their digits. Today's number is the largest of these numbers.
23 December
Arrange the digits 1-9 in a 3×3 square so the 3-digits numbers formed in the rows and columns are the types of numbers given at the ends of the rows and columns.
The number in the first column is today's number.
| | | a multiple of 4 |
| | | a cube |
| | | a multiple of 3 |
| today's number | a cube | an odd number |
22 December
In bases 3 to 9, the number 112 is:
\(11011_3\),
\(1300_4\),
\(422_5\),
\(304_6\),
\(220_7\),
\(160_8\), and
\(134_9\).
In bases 3, 4, 6, 8 and 9, these representations contain no digit 2.
There are two 3-digit numbers that contain no 2 in their representations in all the bases between 3 and 9 (inclusive). Today's number is the smaller of these two numbers.
21 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the smallest number you can make with the digits in the red boxes.
| + | | - | | = 7 |
| ÷ | | - | | ÷ | |
| + | | ÷ | | = 8 |
| × | | × | | × | |
| + | | - | | = 7 |
=
12 | | =
5 | | =
28 | |
Show answer
Hide answer
| 8 | + | 3 | - | 4 | = 7 |
| ÷ | | - | | ÷ | |
| 6 | + | 2 | ÷ | 1 | = 8 |
| × | | × | | × | |
| 9 | + | 5 | - | 7 | = 7 |
=
12 | | =
5 | | =
28 | |
The smallest number you can make with the digits in the red boxes is 123.