Puzzles
Overlapping triangles
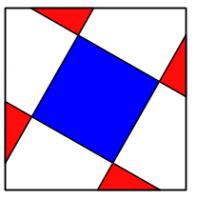
Four congruent triangles are drawn in a square.
The total area which the triangles overlap (red) is equal to the area
they don't cover (blue). What proportion of the area of the large square
does each (purple) triangle take up?
Show answer & extension
Hide answer & extension
Let \(S\) be the area of the large square, \(T\) be the area
of one of the large triangles, \(U\) be one of the red overlaps
and V be the uncovered blue square. We can write
$$S=4T-4U+V$$
as the area of the square is the total of the four triangles,
take away the overlaps as they have been double counted, add
the blue square as it has been missed.
We know that 4U=V, so
$$S=4T-V+V$$
$$S=4T.$$
Therefore one of the triangles covers one quarter of the
square.
Extension
Five congruent triangles are drawn in a regular pentagon. The
total area which the triangles overlap (red) is equal to the area they
don't cover (blue). What proportion of the area of the large pentagon
does each triangle take up?
\(n\) congruent triangles are drawn in a regular \(n\) sided polygon.
The
total
area which the triangles overlap is equal to the area they don't cover.
What proportion of the area of the large \(n\) sided polygon does each
triangle take up?
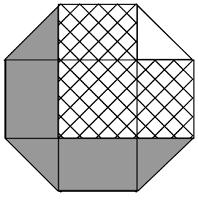
Unit octagon
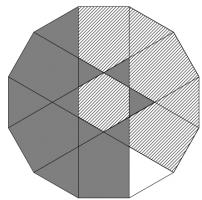
The diagram shows a regular octagon with sides of length 1. The octagon is divided into regions by four diagonals. What is the difference between the area of the hatched region and the area of the region shaded grey?
Show answer & extension
Hide answer & extension
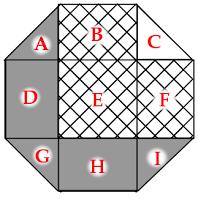
Name the regions as follows:
\(E\) is a 1×1 square. Placed together, \(A\), \(C\), \(G\) and \(I\) also make a 1×1 square. \(B\) is equal to \(H\) and \(D\) is equal to \(F\).
Therefore \(B+E+F=A+C+D+G+H+I\). Therefore the hatched region is \(C\) larger than the shaded region. The area of \(C\) (and therefore the difference) is \(\frac{1}{4}\).
Extension
What is the difference between the shaded and the hatched regions in this dodecagon?
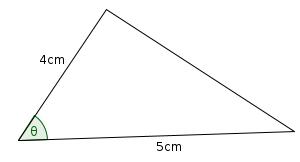
Largest triangle
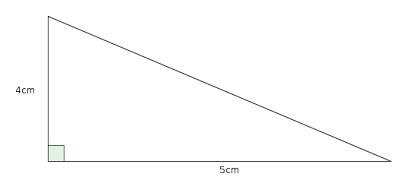
What is the largest area triangle which has one side of length 4cm and one of length 5cm?
Show answer & extension
Hide answer & extension
As our shape is a triangle, the 4cm and 5cm sides must be adjacent. Call the angle between them be \(\theta\).
The area of the triangle is \(\frac{1}{2}\times 4\times 5 \times \sin{\theta}\) or \(10\sin{\theta}\). This has a maximum value when \(\theta=90^\circ\), so the largest triangle has and area of 10cm2 and looks like:
Extension
What is the largest area triangle with a perimeter of 12cm?
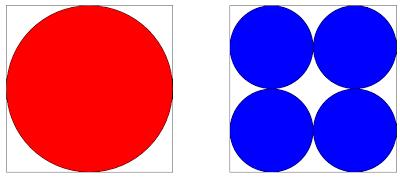
Circles
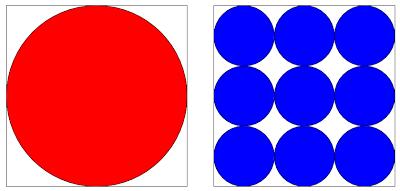
Which is largest, the red or the blue area?
Show answer & extension
Hide answer & extension
Let \(4x\) be the side length of the square. This means that the radius of the red circle is \(2x\) and the radius of a blue circle is \(x\). Therefore the area of the red circle is \(4\pi x^2\).
The area of one of the blue squares is \(\pi x^2\) so the blue area is \(4\pi x^2\). Therefore the two areas are the same.
Extension
Is the red or blue area larger?
Equal areas
An equilateral triangle and a square have the same area. What is the ratio of the perimeter of the triangle to the perimeter of the square?
Show answer & extension
Hide answer & extension
Let \(A\) be the area of the square (and the triangle).
The length of a side of the square is \(\sqrt{A}\), so the perimeter of the square is \(4\sqrt{A}\).
Let \(l\) be the length of a side the triangle. Then \(\frac{1}{2}l^2\sin{60}=A\), so \(l^2=\frac{4A}{\sqrt{3}}\). Therefore \(l=\frac{2\sqrt{A}}{3^\frac{1}{4}}\) and the perimeter of the triangle is \(\frac{6\sqrt{A}}{3^\frac{1}{4}}\).
Hence the ratio of the perimeters is \(\frac{6\sqrt{A}}{3^\frac{1}{4}} : 4\sqrt{A}\) which simplifies to 33/4:2
Extension
If an \(n\) sided regular polygon has the area \(A\), what is the length of one of its sides?