Puzzles
Two tangents
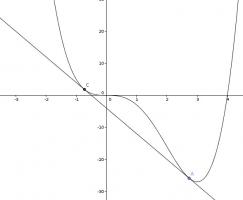
Find a line which is tangent to the curve \(y=x^4-4x^3\) at 2 points.
Show answer
Hide answer
At \(x=a\), \(y=a^4-4a^2\) and \(\frac{dy}{dx}=4a^3-12a^2\). Therefore the equation of the tangent at \(x=a\) will be \(y=(4a^3-12a^2)x+8a^3-3a^4\).
Taking this away from \(y=x^4-4x^3\) gives \(y=x^4-4x^3-(4a^3-12a^2)x-8a^3+3a^4\). We can now look at where this curve is tangent to \(y=0\) and look for a value of \(a\) that makes it tangent at two points.
If this curve is tangent to the \(x\)-axis at \(x=b\), then it will have a repeated root at \(x=b\). We know it is tangent at \(x=a\), so dividing \(x^4-4x^3-(4a^3-12a^2)x-8a^3+3a^4\) by \((x-a)\) twice gives \(x^2+(2a-4)x+3a^2-8a\). We want this to have a repeated root, hence the discriminant, \((2a-4)^2-4(3a^2-8a)\), must be 0.
Solving this gives \(a=1\pm\sqrt3\).
Therefore the equation of the line is \(y=-8x-4\).
A bit of Spanish
Each of the letters P, O, C, M, U and H represent a different digit from 0 to 9.
Which digit does each letter represent?
Show answer & extension
Hide answer & extension
POCO is 4595 and MUCHO is 68925.
Extension
The question could be written as \(POCO\times 15=MUCHO\).
For which values of \(n\) are the letters uniquely defined by \(POCO\times n = MUCHO\)?
Algebraic fractions
Given that
$$\frac{3x+y}{x-3y}=-1$$
what is the value of
$$\frac{x+3y}{3x-y}$$
?
Show answer & extension
Hide answer & extension
$$\frac{3x+y}{x-3y}=-1$$
implies that
$$3x+y=3y-x\\
2x=y$$
This means that
$$\frac{x+3y}{3x-y}=\frac{x+6x}{3x-2x}\\
=\frac{7x}{x}\\=7$$
Extension
Given that
$$\frac{3x+y}{x-3y}=-k$$
what is the value of
$$\frac{x+3y}{3x-y}$$
?
For which values of \(k\) is the answer an integer?
Four integers
\(a\), \(b\), \(c\) and \(d\) are four positive (and non-zero) integers.
$$abcd+abc+bcd+cda+dab+ab+bc+cd+da+ac+bd\\+a+b+c+d=2009$$
What is the value of \(a+b+c+d\)?
Show answer & extension
Hide answer & extension
$$abcd+abc+bcd+cda+dab+ab+bc+cd+da+ac+bd\\+a+b+c+d=(a+1)(b+1)(c+1)(d+1)-1$$
So:
$$(a+1)(b+1)(c+1)(d+1)=2010\\=2\times 3\times 5\times 67$$
Therefore \(a+b+c+d=1+2+4+66=73\).
Extension
Which numbers could 2009 be replaced with so that the problem still has a unique solution?
Times roamin'
What is the product of this series?
$$(x-a)(x-b)(x-c)...(x-z)$$
x to the power of x again
Let \(y=x^{x^{x^{x^{...}}}}\) [\(x\) to the power of (\(x\) to the power of (\(x\) to the power of (\(x\) to the power of ...))) with an infinite number of \(x\)s]. What is \(\frac{dy}{dx}\)?
Show answer & extension
Hide answer & extension
\(y=x^{x^{x^{x^{...}}}}\) so \(y=x^y=e^{y\ln{x}}\).
By the chain and product rules, \(\frac{dy}{dx}=e^{y\ln{x}}(\frac{dy}{dx}\ln{x}+\frac{y}{x})\).
Rearranging, we get \(\frac{dy}{dx}=\frac{ye^{y\ln{x}}}{x(1-e^{y\ln{x}}\ln{x})}\).
This simplifies to \(\frac{dy}{dx}=\frac{x^{x^{x^{x^{...}}}}x^{x^{x^{x^{...}}}}}{x(1-x^{x^{x^{x^{...}}}}\ln{x})}\).
Extension
What would the graph of \(y=x^{x^{x^{x^{...}}}}\) look like?
x to the power of x
If \(x^{x^{x^{x^{...}}}}\) [\(x\) to the power of (\(x\) to the power of (\(x\) to the power of (\(x\) to the power of ...))) with an infinite number of \(x\)s] is equal to 2, what is the value of \(x\)?