Puzzles
15 December
The odd numbers are written in a pyramid.
| (row 1) | 1 | ||||
| (row 2) | 3 | 5 | |||
| (row 3) | 7 | 9 | 11 | ||
| etc. | |||||
What is the mean of the numbers in the 19th row?
14 December
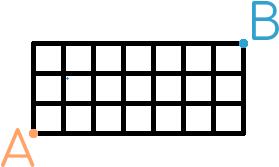
You start at the point marked A in the picture below. You want to get to the point marked B. You may travel to the right, upwards, or to the left along the black lines, but you cannot pass along the same line segment more than once.
Today's number is the total number of possible routes to get from A to B.
13 December
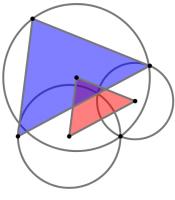
The diagram to the left shows three circles and two triangles. The three circles all meet at one point.
The vertices of the smaller red triangle are at the centres of the circles. The lines connecting the
vertices of the larger blue triangle to the point where all three circles meet are diameters of the
three circles.
The area of the smaller red triangle is 226. What is the area of the larger blue triangle?
12 December
You start at the point marked A in the picture below. You want to get to the point marked B. You may travel to the right or upwards along the black lines.
Today's number is the total number of possible routes to get from A to B.
11 December
The integers are written in a triangle as shown below:
| 1 | ||||||
| 2 | 3 | 4 | ||||
| 5 | 6 | 7 | 8 | 9 | ||
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| etc. | ||||||
Today's number appears directly above the number 750 in the triangle of integers.
10 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct.
Today's number is the largest number you can make using the digits in the red boxes.
| + | + | = 20 | |||
| + | + | + | |||
| + | + | = 10 | |||
| + | + | + | |||
| + | + | = 15 | |||
| = 7 | = 23 | = 15 |
9 December
Eve writes down a sequence of consecutive positive integers (she writes more than one number). The sum of the numbers Eve has written down is 844.
Today's number is the smallest integer that Eve has written down.
8 December
The sum of three integers is 51. The product of the same three integers is 836. What is the product of largest integer and the second-largest integer?