Puzzles
7 December
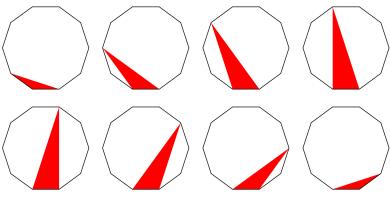
The picture below shows eight regular decagons. In each decagon, a red triangle has been drawn with vertices at three of the vertices of the decagon.
The area of each decagon is 240. What is the total area of all the red triangles?
6 December
When 12345 is divided by today's number, the remainder is 205. When 6789 is divided by today's number, the remainder is 112.
5 December
How many different isosceles triangles are there whose perimeter is 50 units, and whose area is an integer number of square-units?
(Two triangles that are rotations, reflections and translations of each other are counted as the same triangle. Triangles with an area of 0 should not be counted.)
4 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | - | = 5 | |||
| ÷ | × | × | |||
| + | - | = 5 | |||
| - | ÷ | ÷ | |||
| + | × | = 10 | |||
| = -6 | = 18 | = 35 |
3 December
If you write out the numbers from 1 to 1000 (inclusive), how many times will you write the digit 0?
2 December
The number \(7n\) has 37 factors (including 1 and the number itself). How many factors does \(8n\) have?
There was a typo in this puzzle. It originally read "38 factors" when it was meant to say "37 factors".
1 December
The geometric mean of a set of \(n\) numbers can be computed by multiplying together all the numbers then computing the \(n\)th root of the result.
The factors of 4 are 1, 2 and 4. The geometric mean of these is 2.
The factors of 6 are 1, 2, 3, and 6. The geometric mean of these is \(\sqrt{6}\).
The geometric mean of all the factors of today's number is 22.
Advent 2020 logic puzzle
It's nearly Christmas and something terrible has happened: you've just landed in a town in the Arctic circle with a massive bag of letters for Santa, but
you've lost to instructions for how to get to Santa's house near the north pole.
You need to work out where he lives and deliver the letters to him before Christmas is ruined for everyone.
Due to magnetic compasses being hard to use near the north pole, you brought with you a special Advent compass. This compass has nine numbered directions.
Santa has given the residents of the town clues about a sequence of directions that will lead to his house;
but in order to keep his location secret from present thieves,
he gave each resident two clues: one clue is true, and one clue is false.
Here are the clues:
9
"The 4th digit is 4.""The 8th digit is 4."4
"The 3rd digit is 1.""The 4th digit is 7."10
"The 11th digit is a factor of 888.""The 11th digit is a factor of 88."13
"The 3rd digit is 1.""The 4th digit is 6."23
"The 10th digit is 4.""The 10th digit is 3."1
"The last digit is 1, 9 or 5.""The last digit is 1."5
"The 3rd digit is 1.""The 4th digit is 3."16
"The 5th digit is 3.""The 6th digit is 3."11
"The sequence's length is 2+1+6.""The sequence's length is 2×1×6."12
"The 6th to 8th digits are 3, 3, 4.""The 7th to 9th digits are 3, 3, 4."2
"The 7th digit is 4.""The 8th digit is 4."21
"The 5th digit is 3.""The 9th digit is 9."22
"The 9th digit is 9.""The 10th digit is 4."17
"The 3rd digit is 1.""The 4th digit is 9."15
"The 2nd* digit is 7.""The 1st digit is 8."14
"The 1st digit is 7.""The 2nd digit is 7."7
"The last digit is not 5.""The 4th digit is 5."3
"The 11th digit is a factor of 10.""The 11th digit is a factor of 321."6
"The sequence's length is 1+9+2.""The sequence's length is 1×9×2."20
"The 5th digit is 3.""The 5th digit is 4."19
"5 does not appear.""5 appears exactly once."24
"The 3rd digit is 1.""The 4th digit is 8."25
✔18
"The 1st digit is 3, 7 or 8.""The sequence's length is prime."8
"The 3rd digit is 1.""The 4th digit is 2."You can view the map here.