Puzzles
19 December
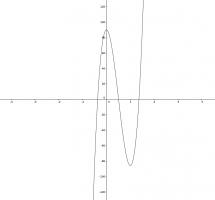
The equation \(352x^3-528x^2+90=0\) has three distinct real-valued solutions.
Today's number is the number of integers \(a\) such that the equation
\(352x^3-528x^2+a=0\) has three distinct real-valued solutions.
![](javascript:showlimage("advent2021-cubic.png"))
18 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | + | = 11 | |||
| + | × | × | |||
| + | + | = 17 | |||
| × | - | + | |||
| + | + | = 17 | |||
| = 11 | = 17 | = 17 |
17 December
The digital product of a number is computed by multiplying together all of its digits.
For example, the digital product of 6273 is 252.
Today's number is the smallest number whose digital product is 252.
16 December
Each clue in this crossnumber is formed of two parts connected by a logical connective:
and means that both parts are true;
nand means that at most one part is true;
or means that at least one part is true;
nor means that neither part is true;
xor means that exactly one part is true;
xnor means that either both parts are false or both parts are true.
No number starts with 0.
|
1A is a palindrome xnor 1D is a palindrome.
1A is greater than 350 nor 1D is less than 150.
3D is odd nand 4A and 2D are equal.
3D is prime xor 5A is odd.
4A is a cube and 2D is a cube.
The sum of the digits of 3D is 2 or the sum of the digits of 5A is 5.
Today's number is 1D.
|
15 December
The odd numbers are written in a pyramid.
| (row 1) | 1 | ||||
| (row 2) | 3 | 5 | |||
| (row 3) | 7 | 9 | 11 | ||
| etc. | |||||
What is the mean of the numbers in the 19th row?
14 December
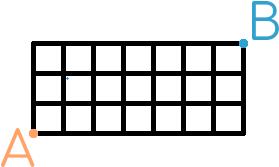
You start at the point marked A in the picture below. You want to get to the point marked B. You may travel to the right, upwards, or to the left along the black lines, but you cannot pass along the same line segment more than once.
![](javascript:showlimage("advent2021-routes.png"))
Today's number is the total number of possible routes to get from A to B.
13 December
![](javascript:showlimage("advent2021-circles.png"))
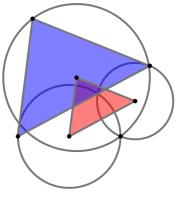
The diagram to the left shows three circles and two triangles. The three circles all meet at one point.
The vertices of the smaller red triangle are at the centres of the circles. The lines connecting the
vertices of the larger blue triangle to the point where all three circles meet are diameters of the
three circles.
The area of the smaller red triangle is 226. What is the area of the larger blue triangle?
12 December
You start at the point marked A in the picture below. You want to get to the point marked B. You may travel to the right or upwards along the black lines.
Today's number is the total number of possible routes to get from A to B.