Puzzles
11 December
The integers are written in a triangle as shown below:
| 1 | ||||||
| 2 | 3 | 4 | ||||
| 5 | 6 | 7 | 8 | 9 | ||
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| etc. | ||||||
Today's number appears directly above the number 750 in the triangle of integers.
10 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct.
Today's number is the largest number you can make using the digits in the red boxes.
| + | + | = 20 | |||
| + | + | + | |||
| + | + | = 10 | |||
| + | + | + | |||
| + | + | = 15 | |||
| = 7 | = 23 | = 15 |
9 December
Eve writes down a sequence of consecutive positive integers (she writes more than one number). The sum of the numbers Eve has written down is 844.
Today's number is the smallest integer that Eve has written down.
8 December
The sum of three integers is 51. The product of the same three integers is 836. What is the product of largest integer and the second-largest integer?
7 December
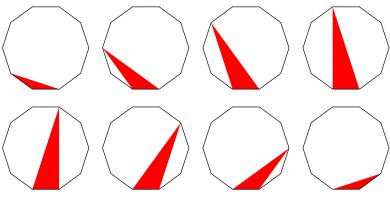
The picture below shows eight regular decagons. In each decagon, a red triangle has been drawn with vertices at three of the vertices of the decagon.
The area of each decagon is 240. What is the total area of all the red triangles?
6 December
When 12345 is divided by today's number, the remainder is 205. When 6789 is divided by today's number, the remainder is 112.
5 December
How many different isosceles triangles are there whose perimeter is 50 units, and whose area is an integer number of square-units?
(Two triangles that are rotations, reflections and translations of each other are counted as the same triangle. Triangles with an area of 0 should not be counted.)
4 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | - | = 5 | |||
| ÷ | × | × | |||
| + | - | = 5 | |||
| - | ÷ | ÷ | |||
| + | × | = 10 | |||
| = -6 | = 18 | = 35 |