Puzzles
6 December
There are 21 three-digit integers whose digits are all non-zero and whose digits add up to 8.
How many positive integers are there whose digits are all non-zero and whose digits add up to 8?
5 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| × | ÷ | = 15 | |||
| + | + | + | |||
| × | ÷ | = 14 | |||
| – | – | – | |||
| × | ÷ | = 27 | |||
| = 9 | = 5 | = 5 |
4 December
The last three digits of \(5^5\) are 125.
What are the last three digits of \(5^{2,022,000,000}\)?
3 December
Write the numbers 1 to 81 in a grid like this:
$$
\begin{array}{cccc}
1&2&3&\cdots&9\\
10&11&12&\cdots&18\\
19&20&21&\cdots&27\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
73&74&75&\cdots&81
\end{array}
$$
Pick 9 numbers so that you have exactly one number in each row and one number in each column,
and find their sum.
What is the largest value you can get?
2 December
What is the smallest number that is a multiple of 1, 2, 3, 4, 5, 6, 7, and 8?
1 December
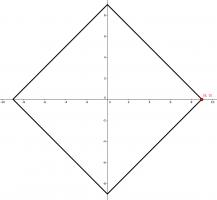
One of the vertices of a rectangle is at the point \((9, 0)\). The \(x\)-axis and \(y\)-axis are both lines of symmetry of the rectangle.
What is the area of the rectangle?
Advent 2021 logic puzzle
It's nearly Christmas and something terrible has happened: a saboteur has infiltrated the stables where Santa's reindeer are kept, and has caused all three of Santa's test flights to be unsuccessful.
You need to help Santa have a successful test flight so that he can deliver presents before Christmas is ruined for everyone.
In order to have enough magical power to fly with the sleigh, all nine of Santa's reindeer must be fed their favourite food. The saboteur gave one or more reindeer the wrong food before each of
the three test flights, causing the reindeer to be unable to take off.
In each clue, "before test flight n" means "immediately before test flight n". Before each test flight, each reindeer was fed exactly one
food, and two or more reindeer may have been fed the same food. Two or more reindeer may have the same favourite food. You must use these clues to work out what each reindeer's favourite food is, then complete a test flight by feeding each reindeer the correct food.
11
Before test flight 2, reindeer 9 was given food 5.
18
Before test flight 2, reindeer 8 was given food 2
2
Before test flight 1, reindeer 2 was given food 4.
9
Before test flight 1, 2 reindeer were given the wrong food.
10
Before test flight 1, reindeer 9 was given food 6
12
Before test flight 3, reindeer 9 was given food 1
19
Before test flight 3, reindeer 5 was not given food 7
21
Before test flight 3, reindeer 7 was given food that is a factor of 148
3
Before test flight 2, reindeer 2 was given food 4.
4
Before test flight 3, reindeer 2 was given food 6.
6
Reindeer 4's favourite food is a factor of 607
13
Before test flight 2, reindeer 4 was not given food 9
20
Before test flight 3, 3 reindeer had the food equal to their number
22
Before test flight 3, reindeer 7 was not given food 1
23
Before test flight 3, no reindeer was given food 2
5
Before test flight 3, 4 reindeer were given the wrong food.
7
Reindeer 4 was given the same food before all three test flights.
14
Before test flight 2, 2 reindeer were given the wrong food
16
Before test flight 2, all the reindeer were given different foods
17
Before test flight 1, reindeer 7 was not given food 7
24
Before test flight 1, reindeer 7 was not given food 9
1
Reindeer 2's favourite food is 4
8
Before test flight 1, reindeer 8 was given food 3.
15
Reindeer 1 was given food 1 before all three test flights
You can attempt a test flight here.
24 December
The digital product of a number is computed by multiplying together all of its digits.
For example, the digital product of 1522 is 20.
How many 12-digit numbers are there whose digital product is 20?