Puzzles
14 December
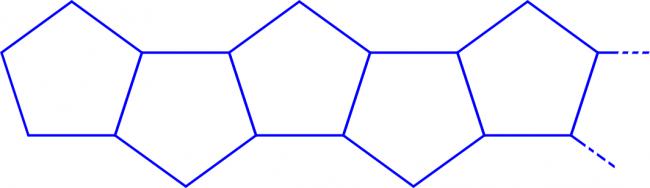
Holly draws a line of connected regular pentagons like this:
She continues the pattern until she has drawn 204 pentagons. The perimeter of each pentagon is 5.
What is the perimeter of her line of pentagons?
Show answer
Hide answer
The two pentagons at the end of the pattern each contribute 4 units to the permimeter. The remaining 202 pentagons each contribute 3 units to the perimeter.
This gives a total perimeter of 2×4+202×3=614.
13 December
Today's number is given in this crossnumber. The across clues are given as normal, but the down clues are given in a random order: you must work out
which clue goes with each down entry and solve the crossnumber to find today's number.
No number in the completed grid starts with 0.
|
|
| Across |
| 1 | A cube number. | (3) |
| 4 | A square number. | (3) |
| 5 | A multiple of 13. | (3) |
|
Down
(in a random order)
|
- Two times 1A.
- A square number.
- Today's number.
|
|
Show answer
Hide answer
1D is "a square number"; 2D is "two times 1A"; 3D is "today's number": today's number is 564.
12 December
The determinant of the 2 by 2 matrix \(\begin{pmatrix}a&b\\c&d\end{pmatrix}\) is \(ad-bc\).
If a 2 by 2 matrix's entries are all in the set \(\{1, 2, 3\}\), the largest
possible deteminant of this matrix is 8.
What is the largest possible determinant of a 2 by 2 matrix whose entries are all in the set
\(\{1, 2, 3, ..., 12\}\)?
Show answer & extension
Hide answer & extension
The largest deteminant will be made by making \(a\) and \(d\) as large as possible (ie 12) and \(b\) and \(c) as small as possible (ie 1). This gives a
determinant of 143.
Extension
The determinant of the 3 by 3 matrix \(\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}\) is \(a(ei-fh)-b(di-fg)+c(dh-eg)\).
If a 3 by 3 matrix's entries are all in the set \(\{1, 2, 3\}\), the largest possible deteminant of this matrix is 28.
What is the largest possible determinant of a 3 by 3 matrix whose entries are all in the set
\(\{1, 2, 3, ..., 12\}\)?
11 December
There are five 3-digit numbers whose digits are all either 1 or 2 and who do not contain
two 2s in a row: 111, 112, 121, 211, and 212.
How many 14-digit numbers are there whose digits are all either 1 or 2 and who do not contain
two 2s in a row?
Show answer
Hide answer
There are two 1-digit numbers whose digits are all either 1 or 2 and who do not contain two 2s in a row (1, and 2).
There are three 2-digit numbers whose digits are all either 1 or 2 and who do not contain two 2s in a row (11, 12, and 21).
There are five 3-digit numbers whose digits are all either 1 or 2 and who do not contain two 2s in a row (111, 112, 121, 211, and 212).
There are eight 4-digit numbers whose digits are all either 1 or 2 and who do not contain two 2s in a row (1111, 1112, 1121, 1211, 1212, 2111, 2112, and 2121).
(It looks like these are the Fibonacci numbers.)
All these numbers either end in a 1, or end in 12. Therefore the \((n+1)\)-digit number can be made by appending a 1 to the end of the \(n\)-digit numbers
or appending a 12 to the end of the \((n-1)\)-digit numbers: so the next term is always the sum of the previous two terms.
Continuing the pattern, we see that there are 987 14-digit numbers are there whose digits are all either 1 or 2 and who do not contain
two 2s in a row.
10 December
A line is tangent to a curve if the line touches the curve at exactly one point.
The line \(y=-160\,000\) is tangent to the parabola \(y=x^2-ax\). What is \(a\)?
Show answer
Hide answer
A line \(y=\text{constant}\) that is tangent to a parabola must be a tangent to the minimum (or maximum) point.
\(y=x^2-ax\) can be rewritten as \(y=(x-a/2)^2-a^2/4\). The minimum of this will be at \(y=-a^2/4\).
If \(-a^2/4=-160\,000\), then \(a\) is 800.
9 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number you can make with the digits in the red boxes.
| + | | + | | = 20 |
| + | | + | | ÷ | |
| + | | – | | = 0 |
| + | | – | | × | |
| ÷ | | × | | = 12 |
=
22 | | =
6 | | =
2 | |
Show answer
Hide answer
| 9 | + | 7 | + | 4 | = 20 |
| + | | + | | ÷ | |
| 5 | + | 1 | – | 6 | = 0 |
| + | | – | | × | |
| 8 | ÷ | 2 | × | 3 | = 12 |
=
22 | | =
6 | | =
2 | |
The largest number you can make with the digits in the red boxes is 532.
8 December
The equation \(x^5 - 7x^4 - 27x^3 + 175x^2 + 218x = 840\) has five real solutions. What is the product of all these solutions?
Show answer & extension
Hide answer & extension
The product of all the solutions is 840.
Expanding \((x-\alpha)(x-\beta)(x-\gamma)(x-\delta)(x-\epsilon)=0\) gives \(x^5 + \dots = \alpha\beta\gamma\delta\epsilon\). As long as the
coefficient of \(x^5\) is 1, the constant term when written like this will be the product of all the solutions (for this to always work, you will need to include repeated solutions and complex solutions.)
Extension
The equation \(x^8 - 19x^7 + 126x^6 - 294x^5 - 231x^4 + 1869x^3 - 1576x^2 - 1556x + 1680=0\) has eight real solutions. What is the product of all these solutions?
7 December
What is the area of the largest triangle that fits inside a regular hexagon with area 952?
Show answer
Hide answer
The vertices of this triangle will be every other vertex of the hexagon: and other triangle can be made larger by moving one of its vertices closer to a vertex of the hexagon.
The area of this triangle is 476.