Puzzles
22 December
Ivy makes a sequence by starting with the number 35, then repeatedly making the next term by reversing the digits of the current number and adding 6.
The first few terms of this sequence are:
What is the first number in Ivy's sequence that is smaller than the previous term?
21 December
In the annual tournament of Christmas puzzles, each player must play one puzzle match
against each other player. Last year there were four entrants into the tournament (A, B, C, and D),
and so 6 matches were played: A vs B, C vs D, A vs D, A vs C, D vs B, and finally B vs C.
This year, the tournament has grown in popularity and 22 players have entered. How many
matches will be played this year?
20 December
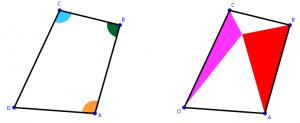
The diagram to the right shows (two copies of) quadrilateral ABCD.
The sum of the angles ABC and BCD (green and blue in quadrilateral on the left) is 180°.
The sum of the angles ABC and DAB (green and orange in quadrilateral on the left) is also 180°.
In the diagram on the right, a point inside the quadrilateral has been used to draw two triangles.
The area of the quadrilateral is 850. What is the smallest that the total area of the two triangles
could be?
19 December
120 is the smallest number with exactly 16 factors (including 1 and 120 itself).
What is the second smallest number with exactly 16 factors (including 1 and the number itself)?
18 December
Noel writes the integers from 1 to 1000 in a large triangle like this:
| 1 | ||||||
| 2 | 3 | 4 | ||||
| 5 | 6 | 7 | 8 | 9 | ||
| 10 | 11 | 12 | 13 | ... |
The number 12 is directly below the number 6. Which number is directly below the number 133?
17 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | + | = 10 | |||
| + | × | × | |||
| + | + | = 12 | |||
| + | – | + | |||
| + | + | = 23 | |||
| = 10 | = 12 | = 23 |
16 December
Noel writes the integers from 1 to 1000 in a large triangle like this:
| 1 | ||||||
| 2 | 3 | 4 | ||||
| 5 | 6 | 7 | 8 | 9 | ||
| 10 | 11 | 12 | 13 | ... |
The rightmost number in the row containing the number 6 is 9.
What is the rightmost number in the row containing the number 300?
15 December
There are 3 even numbers between 3 and 9.
What is the only odd number