Puzzles
Twenty-one
Scott and Virgil are playing a game. In the game the first player says 1, 2 or 3, then the next player can add 1, 2 or 3 to the number and so on. The player who is forced to say 21 or above loses. The first game went like so:
Scott: 3
Virgil: 4
Scott: 5
Virgil: 6
Scott: 9
Virgil: 12
Scott: 15
Virgil 17
Scott: 20
Virgil: 21
Virgil loses.
To give him a better chance of winning, Scott lets Virgil choose whether to go first or second in the next game. What should Virgil do?
Polya strikes out
Write the numbers 1, 2, 3, ... in a row. Strike out every third number beginning with the third. Write down the cumulative sums of what remains:
1, 2, 3, 4, 5, 6, 7, ...
1, 2, 3, 4, 5, 6, 7, ...
1, 2, 4, 5, 7, ...
1=1; 1+2=3; 1+2+4=7; 1+2+4+5=12; 1+2+4+5+7=19; ...
1, 3, 7, 12, 19, ...
Now strike out every second number beginning with the second. Write down the cumulative sums of what remains. What is the final sequence? Why do you get this sequence?
Whist
Messrs. Banker, Dentist, Apothecary and Scrivener played whist last night. (whist is a four player card game where partners sit opposite each other.) Each of these gentlemen is the namesake of another's vocation.
Last night, the apothecary partnered Mr. Apothecary; Mr. Banker's partner was the scrivener; on Mr. Scrivener's right sat the dentist.
Who sat on the banker's left?
Exact change
Source: @AlexDBolton on Twitter
In the UK, the coins less than £1 are 1p, 2p, 5p, 10p, 20p and 50p. How many coins would I need to carry in my pocket so that I could make any value from 1p to 99p?
In the US, the coins less than $1 are 1¢, 5¢, 10¢, 25¢. How many coins would I need to carry in my pocket so that I could make any value from 1¢ to 99¢?
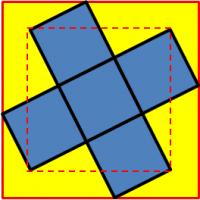
Square cross
Source: Teach Further Maths Blog
![](javascript:showlimage("959058_orig.png"))
A figure in the shape of a cross is made from five 1 x 1 squares, as shown. The cross is inscribed in a large square whose sides are parallel to the dashed square, formed by four vertices of the cross.
What is the area of the large outer square?
![](javascript:showlimage("cross+square.png"))
Ten digit number
Source: Richard Wiseman's Blog
Can you create a 10-digit number, where the first digit is how many zeros in the number, the second digit is how many 1s in the number etc. until the tenth digit which is how many 9s in the number?
Mrs. Coldcream objected
"I object," said Councillor Mrs. Coldcream. "I see no reason why the boys should be so favoured at the expense of the girls."
This was at a meeting of the Holmshire Education Committee. It had been proposed to award 19 scholarships totalling £1000 to boys and girls of the county. It had been proposed that each girl receive a set amount and each boy receive £30 more than each girl.
Mrs. Coldcream pressed her point with such fervour that it was decided to reallocate the money. Each girl would receive £8 more than originally proposed, with the boys' scholarships scaled down accordingly.
How much did each boy and each girl receive?
Cooked turkey
An old invoice showed that seventy-two turkeys had been purchased for "—67.9—". The first and last digits were illegible.
How much did one turkey cost?