Puzzles
Always a multiple?
Take a two digit number. Reverse the digits and add the result to your original number. Your answer is multiple of 11.
Prove that the answer will be a multiple of 11 for any starting number.
Will this work with three digit numbers? Four digit numbers? \(n\) digit numbers?
Show answer & extension
Hide answer & extension
Let the two digit number chosen by \(10a+b\), with \(a\) and \(b\) one digit integers. Reversed this will be \(10b+a\). The sum of these will be \(11a+11b\) which is divisible by 11.
This will work for any integer with an even number of digits. Let our number have \(2n\) digits. It can be written as:
$$\sum_{i=1}^{2n}10^{i-1} a_i $$
Adding it to its reverse, we get:
$$\sum_{i=1}^{2n}10^{i-1} a_i + \sum_{i=1}^{2n}10^{2n-i} a_i = \sum_{i=1}^{2n}(10^{i-1}+10^{2n-i}) a_i $$
\(10^{i-1}+10^{2n-i}\) is divisible by 11 (for \(n \in \mathbb{N}\), \(i \in \mathbb{N}\), \(i\leq 2n\)). This can be shown by induction on \(n\):
If \(n=1\): \(10^{i-1}+10^{2n-i} = 10^{i-1}+10^{2-i}=11\), which is clearly divisible by 11.
Suppose result is true for \(n-1\). Now consider \(10^{i-1}+10^{2n-i}\).
If \(i>1\), then \(10^{i-1}+10^{2n-i}= 10(10^{(i-1)-1}+10^{(2n-2)-(i-1)}\) which is divisible by 11 by the inductive hypothesis.
If \(i=1\), then:
$$10^{i-1}+10^{2n-i} = 1+10^{2n-1} = \sum_{j=1}^{j=2n-2}9\times 10^j +11$$
$$=\sum_{j=1}^{j=n-1}99\times 10^{2j} +11$$
$$=11\left(\sum_{j=1}^{j=n-1}9\times 10^{2j} +1\right)$$
Extension
Which numbers with an odd number of digits will be divisible by 11 when added to their reverse?
Tennis
What is the minimum number of times a player has to hit the ball in a set of tennis and win a standard set (the set is not ended by injury, disqualification, etc.)?
Show answer
Hide answer
A set can be won by hitting the ball 12 times: three service games can be won with four aces, the opponent loses their service games with four double faults.
The mutilated chessboard
You are given a chessboard where two diagonally opposite corners have been removed and a large bag of dominoes of such size that they exactly cover two adjacent squares on the chessboard.
Is it possible to place 31 dominoes on the chessboard so that all the squares are covered? If yes, how? If no, why not?
Show answer & extension
Hide answer & extension
On a normal chessboard there are 32 white and 32 black squares. After removing two diagonally opposite corners there will be 30 white and 32 black or 32 black and 30 white squares.
Each domino covers one white square and one black square. Therefore a combination of dominoes will always cover the same number of black and white squares, so it is not possible to cover all the squares.
Extension
Is it possible to do a
knight's tour on the mutilated chessboard?
Cycling digits
I have in mind a number which when you remove the units digit and place it at the front, gives the same result as multiplying the original number by 2. Am I telling the truth?
Show answer & extension
Hide answer & extension
A few examples are:
$$105263157894736842 \times 2 = 210526315789473684$$
$$210526315789473684 \times 2 = 421052631578947368$$
$$421052631578947368 \times 2 = 842105263157894736$$
Extension
I have in mind a number which when you remove the units digit and place it at the front, gives the same result as multiplying the original number by 3. Am I telling the truth?
Grand piano
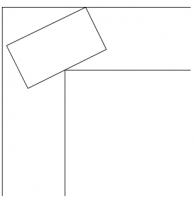
Jack and Jill are moving into a new flat and their grand piano presents a potential problem. Fortunately, it will just pass round the corridor without being tipped or disassembled.
Given that its area, looking down from above, is the largest possible which can be passed around the corner, what is the ratio of its length to its width?
Show answer & extension
Hide answer & extension
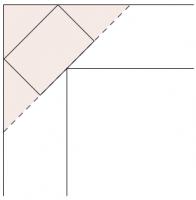
When halfway around the corner, the grand piano will look like this:
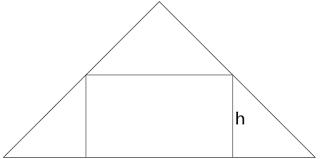
The problem then is finding the largest area rectangle which fits in the highlighted triangle: an isosceles triangle where the base is twice the height. Let the base be 2 and the height be 1.
If the height of the rectangle is \(h\), then its width is \(2(1-h)\). Therefore its area is \(2h-2h^2\). By differentiation, it can be seen that this is maximum when \(h=\frac{1}{2}\), which means that ratio of the rectangle's length to its width is 2:1.
Extension
If the corner was not a 90° angle, then what is the largest area rectangle which could fit round it?
Superdog
A dog is running along a beach at 2m/s. The dog's owner blow a whistle every 10 seconds. Each time the dog hears a whistle, she doubles her speed. How many whistles will the dog hear?
(Hint: speed of sound = 343m/s)
(Hint 2: The answer is not eight!)
Show answer & extension
Hide answer & extension
On hearing the eighth whistle, the dog will be running at 512m/s, faster than the speed of sound. Hence, no more of the master's whistles will reach the dog. However, the dog will catch up with the seven whistles she has already heard and hear them again. So fifteen whistles will be heard in total.
Extension
How much time will the dog have been running for when she hears the final whistle?
Eight peas
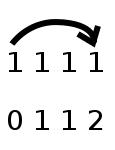
There are eight cups, with one pea in each cup. You are allowed to move a pea by picking up the pea in a pot with only one pea and jumping it to the left or the right over two peas into a pot with only one pea in it. For example, the following moves are allowed:
Starting with your eight cups, can you make four moves?
Times roamin'
What is the product of this series?
$$(x-a)(x-b)(x-c)...(x-z)$$
![](javascript:showlimage("piano.png"))
![](javascript:showlimage("piano-ans.png"))
![](javascript:showlimage("piano-ans2.png"))
![](javascript:showlimage("move1.png"))
![](javascript:showlimage("move2.png"))
![](javascript:showlimage("movesolution.png"))