Puzzles
Mean, median, mode, range
A Find five one-digit positive integers which have a mean of 4, mode of 6, median of 4 and a range of 5.
B Find five one-digit positive integers which have a mean of 3, mode of 1, median of 1 and a range of 8.
C Find five one-digit positive integers which have a mean of 3, mode of 2, median of 2 and a range of 5.
Unit octagon
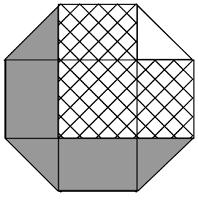
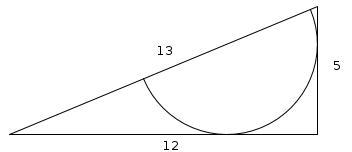
The diagram shows a regular octagon with sides of length 1. The octagon is divided into regions by four diagonals. What is the difference between the area of the hatched region and the area of the region shaded grey?
Show answer & extension
Hide answer & extension
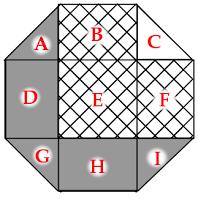
Name the regions as follows:
\(E\) is a 1×1 square. Placed together, \(A\), \(C\), \(G\) and \(I\) also make a 1×1 square. \(B\) is equal to \(H\) and \(D\) is equal to \(F\).
Therefore \(B+E+F=A+C+D+G+H+I\). Therefore the hatched region is \(C\) larger than the shaded region. The area of \(C\) (and therefore the difference) is \(\frac{1}{4}\).
Extension
What is the difference between the shaded and the hatched regions in this dodecagon?
Largest triangle
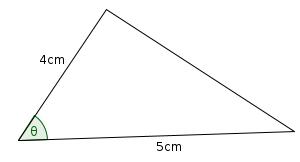
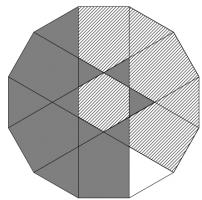
What is the largest area triangle which has one side of length 4cm and one of length 5cm?
Show answer & extension
Hide answer & extension
As our shape is a triangle, the 4cm and 5cm sides must be adjacent. Call the angle between them be \(\theta\).
The area of the triangle is \(\frac{1}{2}\times 4\times 5 \times \sin{\theta}\) or \(10\sin{\theta}\). This has a maximum value when \(\theta=90^\circ\), so the largest triangle has and area of 10cm2 and looks like:
Extension
What is the largest area triangle with a perimeter of 12cm?
Circles
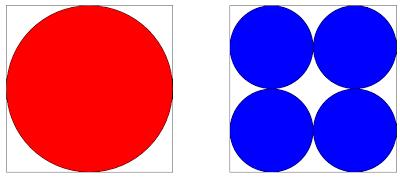
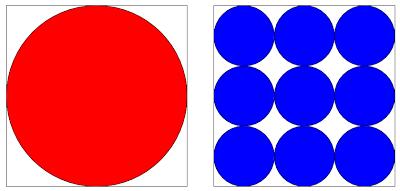
Which is largest, the red or the blue area?
Show answer & extension
Hide answer & extension
Let \(4x\) be the side length of the square. This means that the radius of the red circle is \(2x\) and the radius of a blue circle is \(x\). Therefore the area of the red circle is \(4\pi x^2\).
The area of one of the blue squares is \(\pi x^2\) so the blue area is \(4\pi x^2\). Therefore the two areas are the same.
Extension
Is the red or blue area larger?
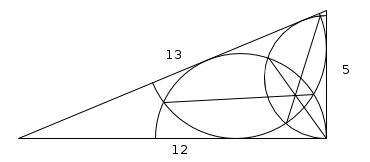
Semi circle in a triangle
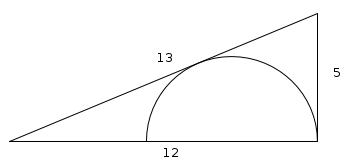
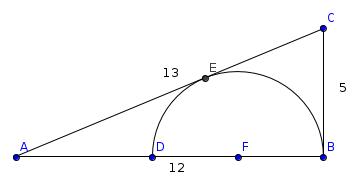
This right-angled triangle above has sides of lengths 12cm, 5cm and 13cm. The diameter of the semicircle lies on the 12cm side and the 13cm side is a tangent to the circle. What is the radius of the semi circle?
Show answer & extension
Hide answer & extension
Label the triangle as follows:
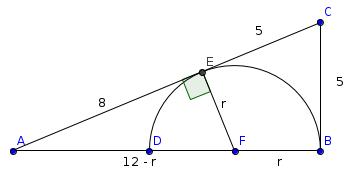
EC and BC are both tangents to the circle so FEA is a right angle and the lengths EC and BC are equal, so the length of EC is 5. Let r be the radius of the circle.
Using Pythagoras' Theorem in triangle FEA:
$$8^2+r^2=(12-r)^2$$
$$64+r^2=144-24r+r^2$$
$$24r=80$$
$$r=\frac{80}{24}=\frac{10}{3}$$
Extension
What is the radius of the circle whose diameter lies on the 5cm side and to which the 12cm and 13cm sides are tangents?
What is the radius of the circle whose diameter lies on the 13cm side and to which the 12cm and 5cm sides are tangents?
Additional observation
For each pair of semi circles, draw a straight line between the two points where the semi circles intersect. These lines all meet at a point.
Light work
"I don't know if you are fond of puzzles, or not. If you are, try this. ... A gentleman (a nobleman let us say, to make it more interesting) had a sitting-room with only one window in it—a square window, 3 feet high and 3 feet wide. Now he had weak eyes, and the window gave too much light, so (don't you like 'so' in a story?) he sent for the builder, and told him to alter it, so as only to give half the light. Only, he was to keep it square—he was to keep it 3 feet high—and he was to keep it 3 feet wide. How did he do it? Remember, he wasn't allowed to use curtains, or shutters, or coloured glass, or anything of that sort."
Lights
You have been taken captive and are blindfolded. There is a table in front of you with four lights on it. Some are on, some are off: you don't know how many and which ones. You need to get either all the lights on or all the lights off to be released. To do this, you can ask your captor to toggle the light switches of some of the lights. You captor will then rotate the table (so you don't know where the lights you toggled now are). Find a sequence of moves which will always lead to your release.
Show answer & extension
Hide answer & extension
If two lights opposite each other are on and the other two are off, then toggling two opposite lights will always lead to your release. It can be checked that the following combination will always lead to this:
- Toggle two opposite lights
- Toggle two adjacent lights
- Toggle two opposite lights
- Toggle one light
- Toggle two opposite lights
- Toggle two adjacent lights
- Toggle two opposite lights
Extension
Can the same be done with eight lights?
Princess problem
A princess lives in a row of 17 rooms. Each day she moves to a room adjacent to the one she wakes up in (eg. If she sleeps in room 5 today, then she will sleep in room 4 or 6 tomorrow). If you are able to find the princess by only opening one door each night then you will become her prince. Can you find her in a finite number of moves?
Show answer & extension
Hide answer & extension
Imagine a chessboard with 17 columns and a large number of rows. Let each column correspond to one of the rooms. In the first row, mark the room in which the princess is. Every day following, mark her location in the next row.
The princess will always move one square diagonally, so will always be on the same colour square she started on. Begin by checking the 17th room, then the 16th room, then continue down the the first room. If the princess started on a black square you will have found her, as she has no way of getting past you.
If you have not caught the princess, then she must have started on a white square. Checking rooms 17 down to one again will find her as this time it will start on a white square.
Extension
Is there a quicker way to find the princess?
![](javascript:showlimage("octagon.png"))
![](javascript:showlimage("octagon-a1.png"))
![](javascript:showlimage("dodecagon.png"))
![](javascript:showlimage("triangle.png"))
![](javascript:showlimage("triangle-biggest.png"))
![](javascript:showlimage("circles.png"))
![](javascript:showlimage("circles-ext.png"))
![](javascript:showlimage("circle-and-triangle.png"))
![](javascript:showlimage("labelled-tricirc.png"))
![](javascript:showlimage("labelled-tricirc2.png"))
![](javascript:showlimage("ext1.png"))
![](javascript:showlimage("ext2.png"))
![](javascript:showlimage("ext3.png"))
