Puzzles
One two three
Each point on a straight line is either red or blue. Show that it's always possible to find three points of the same color in which one is the midpoint of the other two.
Show answer & extension
Hide answer & extension
Pick two points (A and B) of the same colour (say red). Consider the points:
- C such that B is the midpoint of AC.
- D such that A is the midpoint of BD.
- E such that E is the midpoint of AB.
If at least one of C, D or E is red, then three equally spaced red points have been found. If C, D and E are blue, then they are three equally spaced blue points.
Extension
Will there be four equally spaced points of the same colour?
Coloured pins
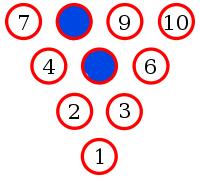
A bowling alley has a mixture of red and blue pins. Ten of these pins are randomly chosen and arranged in a triangle.
Will there always be three pins of the same colour which lie on the vertices of an equilateral triangle?
Show answer & extension
Hide answer & extension
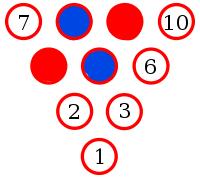
Yes. To show this, let's suppose there is an arrangement of pins with no monochrome triangle.
Let the middle pin be blue (if it is not blue, then swapping all the colours will make it blue without adding/removing monochrome triangles).
Pins 8, 2 and 6 make a triangle. Therefore one of these pins must be blue. By symmetry, any of these situations is equivalent to 8 being blue.
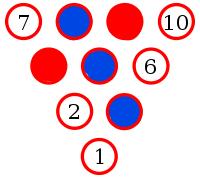
Pins 9 and 4 must be red to prevent a blue triangle.
Pin 3 must be blue to prevent a red triangle.
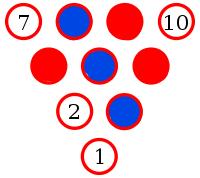
Pin 6 must be red to prevent a blue triangle.
But now whichever colour 10 is, it will make a monochrome triangle. Therefore there must be three pins of the same colour which lie on the vertices of an equilateral triangle.
Extension
What is the smallest \(n\) such that any mixture of \(n^2\) red and blue pins arranged in a square grid must contain four pins of the same colour which lie on the vertices of a square?
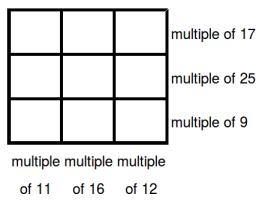
Fill in the digits
Can you place the digits 1 to 9 in the boxes so that the three digit numbers formed in the top, middle and bottom rows are multiples of 17, 25 and 9 (respectively); and the three digit numbers in the left, middle and right columns are multiples of 11, 16 and 12 (respectively)?
The taxman
In a very strange country, the tax system works as follows.
£1, £2, £3 up to £12 are available.
You pick an amount. You keep this amount, but the taxman takes any factors of it. You cannot pick any amount without a factor.
This continues until you can take no more money. The taxman gets any remaining money.
For example, you might play as follows:
- Take £12. Taxman gets £1, £2, £3, £4, £6.
- Take £10. Taxman gets £5.
- You cannot take anything. Taxman gets £7, £8, £9, £11.
In this example, you end with £22 and the taxman ends with
£56.
Is it possible to get more money than the taxman? What is the most you can get?
Show answer & extension
Hide answer & extension
The maximum you can get is £50, with the taxman getting
£28. Here is
how to get it:
- Take £11. Taxman gets £1.
- Take £9. Taxman gets £3.
- Take £8. Taxman gets £2, £4.
- Take £10. Taxman gets £5.
- Take £12. Taxman gets £6.
- You cannot take anything. Taxman gets £7.
Extension
Can you always beat the taxman if £1 up to £\(n\) are
available?
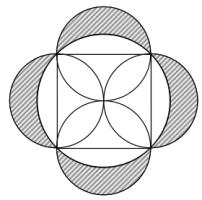
Squared circle
Each side of a square has a circle drawn on it as diameter. The square is also inscribed in a fifth circle as shown.
Find the ratio of the total area of the shaded crescents to the area
of the square.
Show answer
Hide answer
Let the radius of the small circles be \(r\). The are of half of one of these circles is \(\frac{1}{2}\pi r^2\).
The side of the square is \(2r\) and so the area of the square is \(4r^2\). Therefore the area of the whole shape is \((4+2\pi)r^2\).
By Pythagoras' Theorem, the radius of the large circle is \(r\sqrt{2}\). Therefore the area of the circle is \(2\pi r^2\). This means that the shaded area is \((4+2\pi)r^2 - 2\pi r^2\) or \(4r^2\).
This is the same as the area of the square, so the ratio is 1:1.
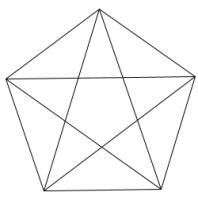
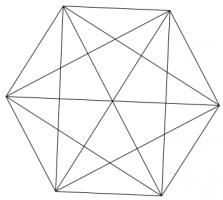
Polygraph
Draw a regular polygon. Connect all its vertices to every other vertex. For example, if you picked a pentagon or a hexagon, the result would look as follows:
Colour the regions of your shape so that no two regions which share an edge are the same colour. (Regions which only meet at one point can be the same colour.)
What is the least number of colours which this can be done with?
Show answer & extension
Hide answer & extension
It can be done with two colours. Let's call these red and blue.
Draw the polygon and colour it red. As each line is added to is, swap the colours on one side of the line which leaving them the same on the other side. At the end of this process you will have any polygon coloured with two colours.
Extension
How many regions will the regular shape be split into by the lines?
The sixth cent
You toss 6 fair coins, and I toss 5 fair coins. What is the probability that you get more heads than I do?
Show answer & extension
Hide answer & extension
As You have one more coin than me, if you don't throw more heads than me, then you must throw more tails than me.
This means that the probability of you throwing more heads then me plus the probability of you throwing more tails then me is equal to one.
By symmetry, the probabilities for heads and tails must be equal and so the probability that you throw more heads is \(\frac{1}{2}\)
Extension
You toss \(n\) fair coins, and I toss \(m\) fair coins. What is the probability that you get more heads than I do?
One hundred factorial
How many zeros does \(100!\) end with?
Show answer & extension
Hide answer & extension
The number of zeros at the end of a number is the same as the number of 10s in the product that makes the number. Each of these 10s is made by multiplying 5 by 2.
There will be more even numbers than multiples of 5 in \(100!\), so the number of 5s will tell us how many zeros the number ends in.
In \(100!\), there will be 20 multiples of 5 and 4 multiples of \(5^2\). This means that \(100!\) will end in 24 zeros.
Extension
How many zeros will \(n!\) end in?
![](javascript:showlimage("one-two-three.png"))
![](javascript:showlimage("bowling-pins.png"))
![](javascript:showlimage("bowling-a1.png"))
![](javascript:showlimage("bowling-a2.png"))
![](javascript:showlimage("bowling-a3.png"))
![](javascript:showlimage("bowling-a4.png"))
![](javascript:showlimage("bowling-a5.png"))
![](javascript:showlimage("chalkdust-puzzle.png"))
![](javascript:showlimage("circles-and-squares.png"))
![](javascript:showlimage("polygraph2.png"))
![](javascript:showlimage("polygraph1.png"))