Puzzles
The self referential crossword
Fill in the following crossnumber grid so that each clue describes the solution.
For example, if some clues read "TEN DS", "ONE X" and "THREE ES" then there will be ten Ds, one X and three Es in the completed grid. The entries in the crossword include the spaces.
Cutting corners
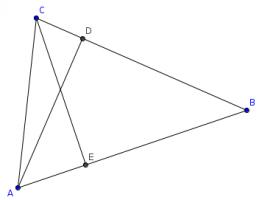
The diagram below shows a triangle \(ABC\). The line \(CE\) is perpendicular to \(AB\) and the line \(AD\) is perpedicular to \(BC\).
The side \(AC\) is 6.5cm long and the lines \(CE\) and \(AD\) are 5.6cm and 6.0cm respectively.
How long are the other two sides of the triangle?
Show answer
Hide answer
Let \(A\), \(B\) and \(C\) represent the angles at points \(A\), \(B\) and \(C\). Looking at triangle \(ACE\) gives:
$$\sin A=\frac{5.6}{6.5}$$
And triangle \(ACD\) gives:
$$\sin C=\frac{6.0}{6.5}$$
Using Pythagoras' Theorem to find the missing sides in these triangles also gives:
$$\cos A=\frac{3.3}{6.5}$$
$$\cos C=\frac{2.5}{6.5}$$
We can use these to find \(\sin B\):
$$\begin{array}{rl}
\sin B&=\sin(\pi-A-C)\\
&=\sin(A+B)\\
&=\sin A\cos C + \cos A\sin C\\
&=\frac{5.6}{6.5}\frac{2.5}{6.5}+\frac{6.0}{6.5}\frac{3.3}{6.5}\\
&=\frac{33.8}{6.5^2}
\end{array}$$
Now the missing sides can be found using the sine rule:
$$\begin{array}{rl}
CB&=\frac{CA\sin A}{\sin B}\\
&=\frac{6.5\times\frac{5.6}{6.5}}{\frac{33.8}{6.5^2}}\\
&=\frac{6.5^2\times5.6}{33.8}\\
&=7\text{cm}
\end{array}$$
$$\begin{array}{rl}
AB&=\frac{CA\sin C}{\sin B}\\
&=\frac{6.5\times\frac{6}{6.5}}{\frac{33.8}{6.5^2}}\\
&=\frac{6.5^2\times6}{33.8}\\
&=7.5\text{cm}
\end{array}$$
Rugby scores
In a rugby (union) match, 3 point are scored for a kick, 5 for a try and 7 for a converted try. This scoring system means that some total scores can be achieved in different combinations, while others can be achieved in only one way.
For example, 14 can be scored in two ways (three kicks and a try; or two converted tries), while 8 can only be achieved in one way (try and a kick).
What is the highest score which can only be made in one way?
What is the highest score which can be made in two ways?
Show answer & extension
Hide answer & extension
11 is the highest score which can only be made in one way (try and two kicks).
Each of 12, 13 and 14 can be made in two ways:
- 12 - try and converted try; or four kicks
- 13 - converted try and two kicks; or two tries and a kick
- 14 - three kicks and a try; or two converted tries
Now any score higher than 14 can be made by adding kicks to one of these three. This gives at least two ways of making every score higher than this.
By a similar argument, it can be shown that 16 is the highest score which can only be made in two ways.
For the highest score which can be made in \(n\) ways, see the OEIS sequence
A261155.
Extension
Which is the highest rugby score such that if the number of tries scored is known, you can always tell how many of these tries were converted?
Quarter circle
Source: Maths Jam
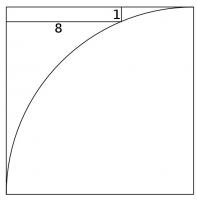
A quarter circle is drawn in a square. A rectangle is drawn in the corner of the square which touches the circle and has sides of length 8 and 1.
What is the length of a side of the square?
Show answer
Hide answer
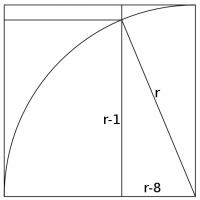
Let the radius of the circle by \(r\). Draw in the following two lines.
The sides of the triangle formed are \(r\), \(r-1\) and \(r-8\). By Pythagoras' Theorem:
$$(r-1)^2+(r-8)^2=r^2$$
$$r^2-2r+1+r^2-16r+64=r^2$$
$$r^2-18r+65=0$$
$$(r-13)(r-5)=0$$
$$r=5\text{ or }13$$
\(r\) must be larger than 8, \(r=13\).
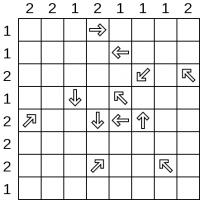
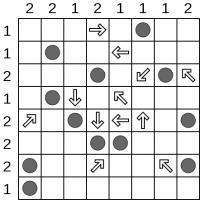
Shinro
In the grid below, there are 12 holes hidden in the grid. Each of the arrows is pointing towards at least one hole. None of the arrows covers a hole.
For example, the arrow in the first row tells you that at least one of the last four squares in that row contains a hole.
Find the location of all 12 holes.
Integer part
Let \(\lfloor x\rfloor \) denote the integer part of \(x\) (eg. \(\lfloor 7.8\rfloor =7\)).
When are the following true:
a) \(\lfloor x+1\rfloor = \lfloor x\rfloor + 1\)
b) \(\lfloor nx\rfloor = n\lfloor x\rfloor\) (where \(n\) is an integer)
c) \(\lfloor x+y\rfloor = \lfloor x\rfloor +\lfloor y\rfloor \)
d) \(\lfloor xy\rfloor = \lfloor x\rfloor \lfloor y\rfloor \)
Show answer & extension
Hide answer & extension
a) Always
b) When \(n<\frac{1}{f_x}\), where \(f_x\) is the fractional part of \(x\).
c) When the fractional parts of \(x\) and \(y\) add up to less than one.
d) Let \(f_x\) and \(f_y\) be the fractional parts of \(x\) and \(y\) (respectively).
$$\lfloor xy\rfloor = \lfloor (\lfloor x\rfloor +f_x)(\lfloor y\rfloor +f_x)\rfloor $$
$$=\lfloor \lfloor x\rfloor \lfloor y\rfloor +f_x\lfloor y\rfloor +f_y\lfloor x\rfloor +f_yf_x\rfloor $$
$$=\lfloor x\rfloor \lfloor y\rfloor +\lfloor f_x\lfloor y\rfloor +f_y\lfloor x\rfloor +f_yf_x\rfloor $$
This will be equal to \(\lfloor x\rfloor \lfloor y\rfloor \) when \(\lfloor f_x\lfloor y\rfloor +f_y\lfloor x\rfloor +f_yf_x\rfloor =0\).
For this to be true, it is necessary (but not sufficient) that \(f_y<\frac{1}{x}\) and \(f_x<\frac{1}{y}\).
Extension
Show that
$$\lfloor x\rfloor +\left\lfloor x+\frac{1}{n}\right\rfloor +\left\lfloor x+\frac{2}{n}\right\rfloor +...+\left\lfloor x+\frac{n-1}{n}\right\rfloor =\lfloor nx\rfloor.$$
Make the sums
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, \(4+3\times2\) is 14, not 10.
| + | | - | | = 4 |
| + | | - | | × | |
| - | | × | | = 27 |
| - | | × | | ÷ | |
| × | | ÷ | | = 16 |
=
2 | | =
8 | | =
6 | |
Show answer & extension
Hide answer & extension
| 1 | + | 5 | - | 2 | = 4 |
| + | | - | | × | |
| 7 | - | 4 | × | 9 | = 27 |
| - | | × | | × | |
| 6 | × | 8 | - | 3 | = 16 |
=
2 | | =
8 | | =
6 | |
Extension
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct.
| + | | - | | = 5 |
| - | | - | | - | |
| + | | ÷ | | = 5 |
| + | | ÷ | | × | |
| + | | × | | = 99 |
=
0 | | =
1 | | =
18 | |