Puzzles
1 December
Eve writes down five different positive integers. The sum of her integers is 16. What is
the product of her integers?
Show answer
Hide answer
The only five different positive integers with a sum of 16 are 1, 2, 3, 4, and 6.
The product of these is 144.
25 December
It's nearly Christmas and something terrible has happened: a machine in Santa's toy factory has malfunctioned, and is unable to finish building all
the presents that Santa needs.
You need to help Santa work out how to fix the broken machine so that he can build the presents and deliver them before Christmas is ruined for everyone.
Inside the broken machine, there were five toy production units (TPUs) installed at sockets labelled A to E. During the malfunction, these TPUs were
so heavily damaged that Santa is unable to identify which TPU they were when trying to fix the machine. The company that supplies TPUs builds 10 different units, numbered from 0 to 9.
You need to work out which of the 10 TPUs needs to be installed in each of the machine's sockets, so that Santa can fix the machine. It may be that two or more of the TPUs are the same.
21
C is not 2.
11
E is not 0.
18
One or more of the TPUs is 1
1
C is 1, 8, or 0.
15
C is 4, 4, or 4.
23
The clues on day 9 and day 23 are false.
12
Exactly 2 of the TPUs is/are even.
8
Exactly two of the TPUs are 2.
17
A is 2 and B is 2.
20
Exactly 4 of the TPUs is/are even.
7
D is 9, 8, or 7.
4
E is 2 or 6.
6
E is 2, 3, or 3.
3
A is 5.
22
E is not 7.
14
C is not 3, 9, or 9.
24
Strictly less than 10 clues are true.
9
The clues on days that are factors of 600 are false.
5
D is 3, 7, or 8.
10
C is 5.
13
E is not 8+1.
19
E is not 5 or 4
2
C is 6, 8, or 1.
16
A is 2 and B is 1.
You can attempt to fix the machine
here.
Show answer
Hide answer
The only way that the clue on day 23 doesn't lead to a contradiction is if clue 23 is false and clue 9 is true. Clue 9 being true means that clues
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, and 24 are all false. So far, we know:
| True clues: | 9 |
| False clues: | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 20, 23, 24 |
| Unknown: | 7, 11, 13, 14, 16, 17, 18, 19, 21, 22 |
Clue 24 being false means that at least 10 of the clues are true, so at most 1 of the unknown clues is false. Clues 16 and 17 contradict each other, so one of these is false and every other
currently unknown clue is true:
| True clues: | 7, 9, 11, 13, 14, 18, 19, 21, 22 |
| False clues: | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 20, 23, 24 |
| Unknown: | 16, 17 |
From the clues we know to be true or false plus knowing that one of 16 and 17 is true, we now know that
A is 2,
B is 1 or 2,
C is 7,
D is 9,
and E is 1 or 8.
We also know that one or more TPU is 1, there are not exactly 2 or exactly 4 even TPUs
and there are not exactly two TPUs that are 2. The last of these clues tell us that B cannot be 2,
and so is 1 and:
| True clues: | 7, 9, 11, 13, 14, 16, 18, 19, 21, 22 |
| False clues: | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 17, 20, 23, 24 |
In order to avoid having exactly 2 even TPUs, E must not be 8, and so
we conclude that A is 2, B is 1, C is 7, D is 9, and E is 1.
24 December
When written in binary, the number 235 is 11101011. This binary representation starts and
ends with 1 and does not contain two 0s in a row.
What is the smallest three-digit number whose binary representation starts and
ends with 1 and does not contain two 0s in a row?
Show answer
Hide answer
- 100 in binary is 1100100;
- 101 in binary is 1100101;
- 102 in binary is 1100110;
- 103 in binary is 1100111;
- 104 in binary is 1101000;
- 105 in binary is 1101001;
- 106 in binary is 1101010;
- 107 in binary is 1101011;
23 December
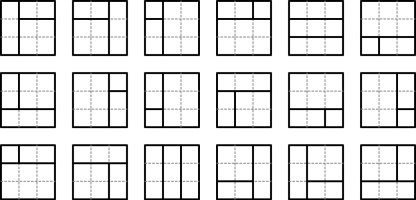
There are 18 ways to split a 3 by 3 square into 3 rectangles whose sides all have integer length:
How many ways are there to split a 10 by 10 square into 3 rectangles whose sides all have integer length?
Show answer
Hide answer
The square is split into 3 rectangles by drawing two lines on the rectangle. There are two cases: the lines can both go
in the same direction; or the lines go in perpendicular directions, with one going all the way across the square and one going from an edge of the square to the other line.
For an \(n\) by \(n\) square, there are:
- \((n-1)(n-2)/2\) ways to pick two dividing lines that are both vertical;
- \((n-1)(n-2)/2\) ways to pick two dividing lines that are both horizontal;
- \(2(n-1)(n-1)\) ways to pick two dividing lines where one is vertical and goes all the way across the square, and the other is horizontal.
- \(2(n-1)(n-1)\) ways to pick two dividing lines where one is horizontal and goes all the way across the square, and the other is vertical;
In total this makes \((n-1)(5n-6)\) ways to split the square. (10–1)×(5×10-6) is 396.
22 December
There are 4 ways to pick three vertices of a regular quadrilateral so that they form a right-angled triangle:
In another regular polygon with \(n\) sides, there are 14620 ways to pick three vertices so that they form a right-angled triangle. What is \(n\)?
Show answer
Hide answer
The vertices of any regular polygon lie on a circle, and so the three vertices we pick must lie on this circle. The triangle will be right-angled
if one of the edges of the triangle is a diameter of the circle.
If the regular polygon has \(n=2k\) sides, then there are \(k\) ways to pick two points that make a diameter, and \(2k-2\) ways to pick the third point to make the triangle, and so there are
a total of \(k(2k-2)=n(n-2)/2\) right-angled triangles. This means that we need to solve \(n(n-2)/2=14620\). The solution is \(n=172\), and so our polygon has 172 sides.
21 December
There are 6 two-digit numbers whose digits are all 1, 2, or 3 and whose second digit onwards
are all less than or equal to the previous digit:
How many 20-digit numbers are there whose digits are all 1, 2, or 3 and whose second digit onwards
are all less than or equal to the previous digit?
Show answer & extension
Hide answer & extension
We can look at how many \(n\)-digit number there are for small values of \(n\) and look for a pattern:
- 1-digit numbers: there are 3.
- 2-digit numbers: there are 6.
- 3-digit numbers: there are 10.
- 4-digit numbers: there are 15.
These are the triangle numbers, and there are 231 20-digit numbers.
Extension
Why is the pattern the triangle numbers?
20 December
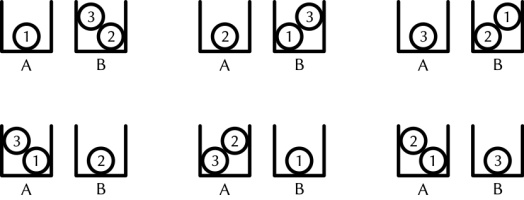
There are 6 different ways that three balls labelled 1 to 3 can be put into two boxes labelled
A and B so that no box is empty:
How many ways can five balls labelled 1 to 5 be put into four boxes labelled A to D so that
no box is empty?
Show answer
Hide answer
One method for putting the five balls into the four boxes is:
pick one of the balls (there are 5 ways to do this), then put the other four balls into boxes with one in each box (there are 4! ways to do this), then
put the picked ball into a box (there are 4 ways to do this). This method gives exactly two ways of obtaining each possible arrangement, so the number of
ways is \(5\times4!\times4\div2\) or 240.
19 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | – | | = 7 |
| × | | × | | × | |
| + | | – | | = 0 |
| ÷ | | ÷ | | ÷ | |
| + | | – | | = 2 |
=
4 | | =
35 | | =
18 | |
Show answer
Hide answer
| 8 | + | 5 | – | 6 | = 7 |
| × | | × | | × | |
| 2 | + | 7 | – | 9 | = 0 |
| ÷ | | ÷ | | ÷ | |
| 4 | + | 1 | – | 3 | = 2 |
=
4 | | =
35 | | =
18 | |
The product of the numbers in the red boxes is 504.