Puzzles
13 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10. Today's number is the smaller number in a red box to the power of the larger number in a red box.
| + | - | = 8 | |||
| - | - | - | |||
| + | ÷ | = 3 | |||
| + | ÷ | × | |||
| + | × | = 120 | |||
| = 8 | = 1 | = 8 |
12 December
Here is a list of facts about today's number:
- If a×b is a factor of it, with a and b both positive integers, then either a or b is one.
- The sum of its digits is 14.
- It is odd.
- The product of its digits is 36.
- It is a palindrome when written in base 9.
- It is smaller than yesterday's number.
- It is 4 more than a multiple of 5.
- It is two less than a prime number.
- It is the number of a bus stopping at Richmond station.
11 December
This year, I have spend a lot of time working on the AVE game engine.
Today's answer is the code to the safe in this Christmas themed game.
10 December
The smallest number that is equal to the sum of its digits
multiplied by ten more than the sum of its digits.
9 December
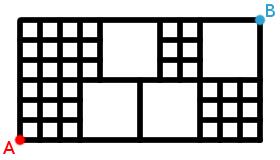
You start at A and are allowed to move either to the right or upwards.
How many different routes are there to get from A to B?
8 December
Today's number is the second smallest number that can be written as
a×b×c×d×e×f×g×h×i, where
a,b,...,i are all integers greater than 1.
7 December
Put the digits 1 to 9 (using each digit once) in the boxes so that the three digit numbers formed (reading left to right and top to bottom) have the desired properties written by their rows and columns.
| multiple of 25 | |||
| today's number | |||
| all digits even | |||
| multiple of 91 | multiple of 7 | cube number |
6 December
When you add up the digits of a number, the result is called the digital sum.
How many different digital sums do the numbers from 1 to 1091 have?*
* There was a mistake in this question (it previously said 1092).
If you answered the typo'd question right, your answer should automatically correct itself to 9 less than it was...