Puzzles
1 December
There are 5 ways to write 4 as the sum of 1s and 2s:
- 1+1+1+1
- 2+1+1
- 1+2+1
- 1+1+2
- 2+2
Today's number is the number of ways you can write 12 as the sum of 1s and 2s.
Show answer
Hide answer
233
Let \(f(n)\) be the number of ways to write \(n\) as the sum of 1s and 2s.
When you write \(n\) as the sum of 1s and 2s, the sum must end in either 1 or 2: if it ends in 1, then there are \(f(n-1)\) ways to write the
rest before this 1 as the sum of 1s and 2s; if it ends in 2, there are \(f(n-2)\) ways to write the rest.
This means that \(f(n)=f(n-1)+f(n-2)\), or in other words the Fibonacci numbers.
Cryptic crossnumber #2
In this puzzle, the clues are written like clues from a cryptic crossword, but the answers are all numbers. You can download a printable pdf
of this puzzle
here.
Across| 1 | Found your far dented horn mixed to make square. | (3) | | 3 | Eno back in Bowie's evening prime. | (2) | | 4 | Prime legs. | (2) | | 5 | Palindrome ends cubone, starts ninetales, inside poison ekans. | (3) |
| | Down| 1 | Odd confused elven elves hounded deerhound antenna. | (5) | | 2 | Prime try of confused Sven with Beckham's second. | (2) | | 4 | Prime even and Ian fed the being. | (2) |
|
Show answer
Hide answer
Across
1 Found your far dented horn mixed to make square. (3) — 144 is a square number that is an an anagram of "Found your far dented horn" (one hundred and Forty four).
3 Eno back in Bowie's evening prime. (2) — 17 is a prime that is Eno backwards (onE) followed by a number in Bowie's evening.
4 Prime legs. (2) — 11 is a prime number and called legs in bingo.
5 Palindrome ends cubone, starts ninetales, inside poison ekans. (3) — 191 is a palindrome that is a the end of cubone the start of ninetales and inside poison ekans.
Down
1 Odd confused elven elves hounded deerhound antenna. (5) — 11111 is an odd number that is an anagram of "elven elves hounded deerhound antenna" (eleven thousand one hundred and eleven).
2 Prime try of confused Sven with Beckham's second. (2) — 47 is a prime that is an anagram of "try of" (forty) and Sven with Beckham's second (Seven).
4 Prime even and Ian fed the being. (2) — 19 is a prime number that is the even letters of "and Ian fed the being" (nIneteen).
Cryptic crossnumber #1
In this puzzle, the clues are written like clues from a cryptic crossword, but the answers are all numbers. You can download a printable pdf of this puzzle
here.
Across| 1 | Triangular one then square. | (3) | | 3 | Audible German no between tutus, for one square. | (5) | | 5 | Irreducible ending Morpheus halloumi fix, then Trinity, then mixed up Neo. | (3) |
| | Down| 1 | Inside Fort Worth following unlucky multiple of eleven. | (3) | | 2 | Palindrome two between two clickety-clicks. | (5) | | 4 | Confused Etna honored thundery din became prime. | (3) |
|
Show answer
Hide answer
Across
1 Triangular one then square. (3) — 136 is a triangular number that is a one followed by a square number (36).
3 Audible German no between tutus, for one square. (5) — 29241 is a square number that sounds like a German no (nein/nine) between tutus (two two) for one (four one).
5 Irreducible ending Morpheus halloumi fix, then Trinity, then mixed up Neo. (3) — 631 is an irreducible number that is the ending of Morpheus halloumi fix (six), the trinity (three), then mixed up Neo (oNe).
Down
1 Inside Fort Worth following unlucky multiple of eleven. (3) — 132 is a multiple of 11 that is inside Fort Worth (two) following unlucky (13).
2 Palindrome two between two clickety-clicks. (5) — 66266 is a palindrome that is a two between two clickety-clicks (66s).
4 Confused Etna honored thundery din became prime. (3) — 131 is a prime that is an anagram of "Etna honored thundery din" (onE hundred and thirty one).
Breaking Chocolate
You are given a bar of chocolate made up of 15 small blocks arranged in a 3×5 grid.
You want to snap the chocolate bar into 15 individual pieces. What is the fewest number of snaps that you need to break the bar? (One snap consists of picking up one piece of chocolate and snapping it into two pieces.)
Show answer
Hide answer
Each snap increases the total number of pieces by one. So in order to make 15 pieces, you will need to perform 14 snaps.
Square and cube endings
Source: UKMT 2011 Senior Kangaroo
How many positive two-digit numbers are there whose square and cube both end in the same digit?
Show answer & extension
Hide answer & extension
Only the units digit of the number will affect the last digit of the square and cube. This table shows how the last digits of the square and cube depend on the last digit of the number:
| Last digit of... |
| number | square | cube |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 7 |
| 4 | 6 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| 7 | 9 | 3 |
| 8 | 4 | 2 |
| 9 | 1 | 9 |
So numbers ending in 0, 1, 5 and 6 will have squares and cubes that end in the same digit. There are 4×9=36 two-digit numbers then end in one of these digits.
Extension
How many two-digit numbers are there in binary whose square and cube end in the same digit?
How many two-digit numbers are there in ternary whose square and cube end in the same digit?
How many two-digit numbers are there in base \(n\) whose square and cube end in the same digit?
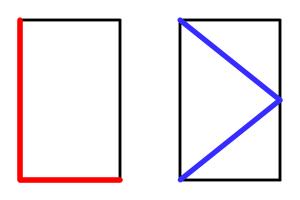
Equal lengths
The picture below shows two copies of the same rectangle with red and blue lines. The blue line visits the midpoint of the opposite side. The lengths shown in red and blue are of equal length.
What is the ratio of the sides of the rectangle?
Show answer
Hide answer
Let \(a\) be the height of the rectangle and \(b\) be the width.
The length of the red line is \(a+b\). The length of the blue line is \(2\sqrt{a^2+\frac{b^2}4}\). These are equal so:
\begin{align}
a+b&=2\sqrt{a^2+\frac{b^2}4}\\
(a+b)^2&=4\left(a^2+\frac{b^2}{4}\right)\\
a^2+2ab+b^2&=4a^2+b^2\\
0&=3a^2-2ab\\
0&=3a-2b\\
2b&=3a
\end{align}
Therefore the ratio of the sides is 2:3.
Digitless factor
Ted thinks of a three-digit number. He removes one of its digits to make a two-digit number.
Ted notices that his three-digit number is exactly 37 times his two-digit number. What was Ted's three-digit number?
Show answer & extension
Hide answer & extension
Ted's number was 925: \(925\div25=37\).
If Ted had removed the final digit of his number, then he would be looking for a solution of \(ABC = 37\times AB\). But \(ABC\)
is between 10 and 11 times \(AB\) (it is \(10\times AB + C\)) and so cannot be 37 times \(AB\). So Ted cannot have removed the final digit.
Therefore, Ted must have removed one of the first two digits: so two- and three- digit numbers have the same final digit (\(C\)).
The final digit of the three-digit number (\(C\)) will be the final digit of \(7\times C\) (7 times the final digit of the two digit number).
This is only possible if the final digit is \(C\) is 0 or 5.
This only leaves four possible solutions—10, 15, 20 and 25—as \(30\times37>1000\). Of these only \(925=37\times25\) works.
Extension
How many three-digit numbers are there that are a multiple of one of the two-digit numbers you can make by removing a digit?
Backwards fours
If A, B, C, D and E are all unique digits, what values would work with the following equation?
$$ABCCDE\times 4 = EDCCBA$$
Show answer
Hide answer
EDCCBA is a multiple of four, so A is even. A cannot be more than 2, as otherwise EDCCBA would have more digits. So A is 2.
E must therefore be 8 or 9 (as 4 times B is less than E) and 3 or 8 (as 4 times E ends in 2). Therefore E is 8.
Carrying on like this, we find:
$$219978\times4=879912$$