Puzzles
12 December
Holly picks a three-digit number. She then makes a two-digit number by removing one of the digits.
The sum of her two numbers is 309. What was Holly's original three-digit number?
Show answer
Hide answer
Holly's sum is odd, so she must have removed the units digit and so her calculation was:
$$
\begin{array}{cccc}
a&b&c\\
&a&b&+\\
\hline
3&0&9
\end{array}
$$
\(a\) and \(b\) cannot both be 0, so the must sum in the tens column must've caused a carry into the hundreds column. This means that \(a\) must be 2, and the calculation is:
$$
\begin{array}{cccc}
2&b&c\\
&2&b&+\\
\hline
3&0&9
\end{array}
$$
Two single digits cannot add to 19, so there can't be a carry from the units column into the tens column. This means that \(b\) is 8:
$$
\begin{array}{cccc}
2&8&c\\
&2&8&+\\
\hline
3&0&9
\end{array}
$$
We can see now that \(c\) was 1, so Holly's three digt number was 281.
11 December
There are 6 sets of integers between 1 and 5 (inclusive) that contain an odd number of numbers whose median value is 3:
- {3}
- {1,3,4}
- {2,3,4}
- {1,3,5}
- {2,3,5}
- {1,2,3,4,5}
How many sets of integers between 1 and 11 (inclusive) are there that contain an odd number of numbers whose median value is 5?
Show answer
Hide answer
If the set contains one number, then it must be {5}.
If the set contains three numbers, then it must contain 5, one number less than 5, and one number greater than 5. There are 4 numbers less than 5 and 6 numbers greater than 5 to choose from, giving
a total of 4×6 = 24 sets.
More generally, if the set contains \(2n+1\) numbers, then it must contain 5, \(n\) numbers less than 5, and \(n\) numbers greater than 5.
There are \(\left(\begin{array}{c}4\\n\end{array}\right)\) numbers less than 5 and \(\left(\begin{array}{c}6\\n\end{array}\right)\) numbers greater than 5 to choose from, giving
a total of \(\left(\begin{array}{c}4\\n\end{array}\right)\times\left(\begin{array}{c}6\\n\end{array}\right)\) sets.
In total there are
$$
1+24+
\left(\begin{array}{c}4\\2\end{array}\right)\times\left(\begin{array}{c}6\\2\end{array}\right)
+
\left(\begin{array}{c}4\\3\end{array}\right)\times\left(\begin{array}{c}6\\3\end{array}\right)
+
\left(\begin{array}{c}4\\4\end{array}\right)\times\left(\begin{array}{c}6\\4\end{array}\right)
$$
sets. This is equal to 210.
10 December
A number is a palindrome if it's the same when its digits are written in reverse order.
What is the sum of all the numbers between 10 and 100 that are palindromes?
Show answer
Hide answer
The palindromes between 10 and 100 will be the numbers 11, 22, 33, ..., 99. The sum of these is 495.
9 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| – | | + | | = 8 |
| – | | ÷ | | ÷ | |
| + | | × | | = 9 |
| × | | ÷ | | ÷ | |
| ÷ | | × | | = 9 |
=
12 | | =
1 | | =
3 | |
8 December
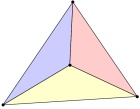
It is possible to arrange 4 points on a plane and draw non-intersecting lines
between them to form 3 non-overlapping triangles:
It is not possible to make more than 3 triangles with 4 points.
What is the maximum number of non-overlapping triangles that can be made by arranging 290 points on a plane
and drawing non-intersecting lines between them?
Show answer
Hide answer
By adding a point inside a triangle, you can turn one triangle into three triangles. By adding a point outside all the current triangles, you can add either
one or two more triangles. As we are after the maximum number of triangles, we will choose to add two triangles for each point we add.
Four points make 3 triangles. Adding 286 more points will add 572 more triangles, giving a total of 575.
7 December
What is the obtuse angle in degrees between the minute and hour hands of a clock at 08:22?
Show answer
Hide answer
Every hour, the hour hand moves 360÷12 = 30°.
Every minute, the hour hand moves 30÷60 = ½° and the minute hand moves 360÷60 = 6°.
At 8:22, the hour hand will be 8×30+22×½ = 251° from the top of the clock
and the minute hand will be 22×6 = 132° from the top of the clock. The angle between the hands will
be 251-132 = 119°.
6 December
The number n has 55 digits. All of its digits are 9.
What is the sum of the digits of n3?
Show answer
Hide answer
We can look for a pattern as we increate the number of 9s that make up n:
| n | n3 |
| 9 | 729 |
| 99 | 970299 |
| 999 | 997002999 |
| 999 | 999700029999 |
| 9999 | 999970000299999 |
If n has k digits, then n3 is
k-1 9s,
followed by a 7,
followed by k-1 0s,
followed by a 2,
followed by k 9s,
The sum of all these digits will by 18k.
Hence, the answer is 18×55 = 990.
5 December
The sum of 11 consecutive integers is 2024. What is the smallest of the 11 integers?
Show answer
Hide answer
Call the smallest number \(n\). The sum of the 11 integers is:
$$n + (n+1) + (n+2) + \dots + (n+10)$$
This simplifies to:
$$11n +55$$
If \(11n+55=2024\), then \(n\) is 179.