Puzzles
20 December
18 can be written as the sum of 3 consecutive (strictly) positive integers: 5 + 6 + 7.
18 can also be written as the sum of 4 consecutive (strictly) positive integers: 3 + 4 + 5 + 6.
18 is in fact the smallest number that can be written as the sum of both 3 and 4 consecutive (strictly) positive integers.
Today's number is the smallest number that can be written as the sum of both 12 and 13 consecutive (strictly) positive integers.
Show answer
Hide answer
The sum of 13 consecutive integers is 13 times the middle number, so today's number is a multiple of 13.
The sum of 12 consecutive integers is 6 times the sum of the two middle numbers, so today's number is also a multiple of 6.
Therefore today's number is a multiple of 78.
78 and 156 do not work (the numbers would not all be strictly positive), so today's number is 234.
19 December
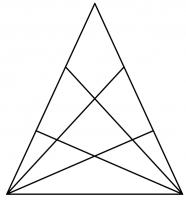
The diagram to the right shows a triangle. Two of the sides of the triangle have been split into three pieces, with lines drawn from the opposite vertex. In total, the diagram now contains 27 triangles of any size.
Another triangle has two of its sides split into eight pieces, with lines drawn from the opposite vertex. How many triangles (of any size) would this create?
Show answer
Hide answer
Each triangle must include one of the two corners at the base of the largest triangle (or both those corners).
To make triangles including the bottom left corner of the large triangle, we must pick two lines coming out of that corner, and one line coming out of the bottom right corner that is not the base of the triangle.
There are 9 lines coming out of the corners, so the total number of triangles is \(\left(\begin{array}{c}9\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=288\).
We now need to count the triangles that include the bottom right corner of the large triangle, but do not include both corners (as we've already counted thoses).
There are \(\left(\begin{array}{c}8\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=224\) ways to pick lines to make these triangles.
In total, this makes 512 triangles.
18 December
The expansion of \((x+y+z)^3\) is
$$x^3 + y^3 + z^3 + 3x^2y + 3x^2z + 3xy^2 + 3y^2z + 3xz^2 + 3yz^2 + 6xyz.$$
This has 10 terms.
Today's number is the number of terms in the expansion of \((x+y+z)^{26}\).
Show answer
Hide answer
In each term, the powers of \(x\), \(y\) and \(z\) must add to 26: the terms will be of the form \(x^iy^jz^{26-i-j}\).
If \(i=0\), there are 27 choices for \(j\) (0 to 26).
If \(i=1\), there are 26 choices for \(j\) (0 to 25).
If \(i=2\), there are 25 choices for \(j\) (0 to 24).
...
If \(i=26\), there is 1 choice for \(j\) (0).
Therefore the total number of terms is 27+26+25+...+1 = 378.
17 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums and product are correct.
Today's number is the product of the numbers in the red boxes.
| + | | + | | = 16 |
| + | | + | | + | |
| + | | + | | = 8 |
| + | | + | | + | |
| × | | × | | = 288 |
=
11 | | =
14 | | =
20 | |
Show answer
Hide answer
| 6 | + | 3 | + | 7 | = 16 |
| + | | + | | + | |
| 1 | + | 2 | + | 5 | = 8 |
| + | | + | | + | |
| 4 | × | 9 | × | 8 | = 288 |
=
11 | | =
14 | | =
20 | |
The product of the numbers in the red boxes is 189.
16 December
Solve the crossnumber to find today's number. No number starts with 0.
|
|
| Across |
| 1 | 3 more than a multiple of 110. | (3) |
| 4 | Today's number. | (3) |
| 5 | 30 more than a multiple of 101. | (3) |
| Down |
| 1 | 37 times the sum of 1A's digits. | (3) |
| 2 | 3 times a factor of 5A. | (3) |
| 3 | 3 less than a multiple of 112. | (3) |
|
15 December
When talking to someone about this Advent calendar, you told them that the combination of XMAS and MATHS is GREAT.
They were American, so asked you if the combination of XMAS and MATH is great; you said SURE. You asked them their name; they said SAM.
Each of the letters E, X, M, A, T, H, S, R, U, and G stands for a different digit 0 to 9. The following sums are correct:
Today's number is SAM. To help you get started, the letter T represents 4.
14 December
The numbers 33, 404 and 311 contain duplicate digits. The numbers 120, 15 and 312 do not.
How many numbers between 10 and 999 (inclusive) contain no duplicate digits?
Show answer
Hide answer
There are 81 two-digit numbers with no duplicate digits: there are 9 choices of tens digit (1 to 9), and for each of these there are 9 remaining choices
for the units digit (0 to 9 but not the number already used).
There are 648 three-digit numbers with no duplicate digits: there are 9 choices of hundreds digit (1 to 9), and for each of these there are 9 remaining choices
for the tens digit (0 to 9 but not the number already used) and 8 choices for the units digit (0 to 9 but neight number already used).
648+81 = 729.
13 December
There are 6 ways to split the sequence of the numbers 1 to 5 into three shorter sequences:
- 1 and 2 and 3, 4, 5
- 1 and 2, 3 and 4, 5
- 1 and 2, 3, 4 and 5
- 1, 2 and 3 and 4, 5
- 1, 2 and 3, 4 and 5
- 1, 2, 3 and 4 and 5
Today's number is the number of ways to split the sequence of the numbers 1 to 10 into five shorter sequences.
Show answer
Hide answer
There are 9 gaps between the numbers 1 to 10. We need to pick 5 of these gaps to split the sequence. There are \(\left(\begin{array}{c}9\\5\end{array}\right)\) ways to do this:
this is 126.