Sunday Afternoon Maths XXII
Overlapping triangles
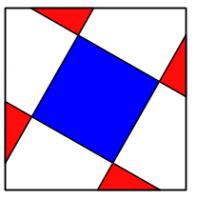
Four congruent triangles are drawn in a square.
The total area which the triangles overlap (red) is equal to the area
they don't cover (blue). What proportion of the area of the large square
does each (purple) triangle take up?
Show answer & extension
Hide answer & extension
Let \(S\) be the area of the large square, \(T\) be the area
of one of the large triangles, \(U\) be one of the red overlaps
and V be the uncovered blue square. We can write
$$S=4T-4U+V$$
as the area of the square is the total of the four triangles,
take away the overlaps as they have been double counted, add
the blue square as it has been missed.
We know that 4U=V, so
$$S=4T-V+V$$
$$S=4T.$$
Therefore one of the triangles covers one quarter of the
square.
Extension
Five congruent triangles are drawn in a regular pentagon. The
total area which the triangles overlap (red) is equal to the area they
don't cover (blue). What proportion of the area of the large pentagon
does each triangle take up?
\(n\) congruent triangles are drawn in a regular \(n\) sided polygon.
The
total
area which the triangles overlap is equal to the area they don't cover.
What proportion of the area of the large \(n\) sided polygon does each
triangle take up?
Coming and going
In my house are a number of rooms. (A hall separated from the rest of the house by one or more doors counts as a room.) Each room has an even number of doors, including doors that lead outside. Is the total number of outside doors even or odd?
Show answer & extension
Hide answer & extension
Add up the number of doors leaving each room; call the sum
\(S\).
As
the number in each room is even, \(S\) will be even. Each interior door
has
been counted twice (as they can be seen in two rooms) and each exterior
door has been counted once. Let \(I\) be the number of interior doors
and
\(E\)
be the number of exterior doors. We have:
$$S=2I+E$$
$$E=S-2I$$
\(S\) and \(2I\) are even, so \(E\) must be even.
Extension
If the number of doors in each room is odd, is the number of
exterior doors odd or even?
![](javascript:showlimage("overlapping1.png"))
![](javascript:showlimage("overlapping2.png"))
