Sunday Afternoon Maths XLIV
Rotating round table
At a large dinner, 24 people are to sit evenly spaced around a round table. Place cards are laid to show where everyone should sit. Unfortunately nobody notices the name cards and the guests sit down with nobody in the correct seat.
Show that it is possible to rotate the table so that at least two people will be in the correct seats.
Show answer & extension
Hide answer & extension
Let \(p(n)\) denote the number of people in the correct seat when the table is rotated by \(n\) people. From the question, we know that:
$$p(0)=0$$
As every guest can be put into the correct place by one rotation, we know that:
$$p(0)+p(1)+...+p(23)=24$$
As \(p(0)=0\):
$$p(1)+...+p(23)=24$$
This sum has 23 positive integers adding up to 24, so one of the rotations must lead to at least two people being in the correct places.
Extension
If the 24 guests sat randomly and one person was in the correct seat, could you still rotate the table so that two people are correctly seated?
Balanced sets
A set of points in the plane is called 'balanced' if for any two points \(A\) and \(B\) in the set, there is another point \(C\) in the set such that \(AC=BC\) (here \(AC\) is the distance between \(A\) and \(C\)).
For all \(n\geq3\), find a balanced set of \(n\) points.
Show answer
Hide answer
If \(n\) is odd, the vertices of a regular \(n\)-gon are balanced.
If \(n\) is even, a balanced set can be constructed as follows:
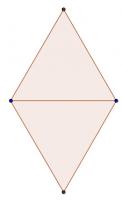
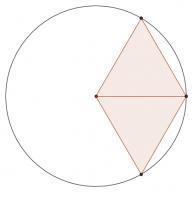
If \(n=4\), this set is balanced (both the triangles are equilateral):
Draw a triangle with its centre at one of the points, going through the other three points:
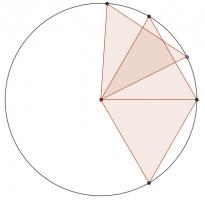
For \(n>4\), repeatedly add a two new points on the circle which form an equilateral triangle with the centre. For example, for \(n=6\), this set is balanced:
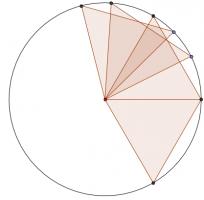
And for \(n=8\), this set is balanced:
121
Find a number base other than 10 in which 121 is a perfect square.
![](javascript:showlimage("balanced-a1.png"))
![](javascript:showlimage("balanced-a1andahalf.png"))
![](javascript:showlimage("balanced-a2.png"))
![](javascript:showlimage("balanced-a3.png"))