Puzzles
20 December
p(x) is a polynomial with integer coefficients such that:
- p(0) > 0;
- if x is a real number,
4x – 9 < p(x) < x2 – 2x + 2.
What is p(23)?
Show answer
Hide answer
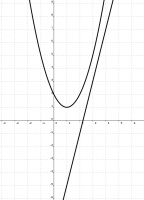
Plotting \(y = 4x - 9\) and \(y = x^2-2x+2\) gives:
As \(p(x)\) has integer coefficients, \(p(3)\) must be an integer. If you click to view a larger version of the image, you'll see that the only option for \(p(3)\) that satisfies
\(4x-9<p(x)<x^2-2x+2\) is \(p(3)=4\).
As \(p(x)>4x-9\), it must at least a polynomial of degree 1. As \(p(x)<x^2-2x+2\), it must be at most a polynomial of degree 2. Playing with coefficients, you can see that
\(p(x)\) is either \(x^2-2x+1\) or \(4x-8\). \(4x-8\) is negative when \(x=0\), so \(p(x)=x^2-2x+1\) and \(p(23)\) is 484.
19 December
There are 9 integers below 100 whose digits are all non-zero and add up to 9:
9, 18, 27, 36, 45, 54, 63, 72, and 81.
How many positive integers are there whose digits are all non-zero and add up to 9?
Show answer & extension
Hide answer & extension
All the integers whose digits are all non-zero and add up to 9 can be made by taking a list of 9 ones, and between each pair deciding whether to move on a digit or not. For example,
1111|111|11 (where | means move on) would represent the number 432; and 1|1|1111111 would represent the number 117.
There are 8 gaps between 9s, so there are 28 = 256 numbers that can be made.
Extension
Why are there not 512 positive integers whose digits are all non-zero and add up to 10?
18 December
If k = 21, then 28k ÷ (28 + k) is an integer.
What is the largest integer k such that 28k ÷ (28 + k) is an integer?
Show answer
Hide answer
If \(k\) is a multiple of 28, then let \(k=28a\) and see that:
$$\frac{28k}{28+k}=\frac{28a}{1+a}$$
This is an integer if either \(a=0\), \(a=1\), or \(1+a\) is a factor of 28. Hence the largest value of \(a\) is 27, leading to \(k\) = 756.
Similar working out can be done for the cases where the hcf of 28 and \(k\) is 14, 7, 2, or 1, and in each case a lower answer would be obtained.
17 December
The number 40 has 8 factors: 1, 2, 4, 5, 8, 10, 20, and 40.
How many factors does the number 226×5×75×112 have?
Show answer
Hide answer
The factors will all be of the form \(2^a\times5^b\times7^c\times11^d\), where
\(0\leqslant a\leqslant26\),
\(0\leqslant b\leqslant1\),
\(0\leqslant c\leqslant5\), and
\(0\leqslant d\leqslant2\). There are 27 choices for \(a\), 2 for \(b\), 6 for \(c\), and 3 for \(d\) giving a total of 27×2×6×3 = 972 factors.
16 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| × | | + | | = 46 |
| ÷ | | + | | + | |
| + | | ÷ | | = 1 |
| ÷ | | × | | × | |
| – | | ÷ | | = 1 |
=
1 | | =
12 | | =
45 | |
Show answer
Hide answer
| 8 | × | 5 | + | 6 | = 46 |
| ÷ | | + | | + | |
| 2 | + | 7 | ÷ | 9 | = 1 |
| ÷ | | × | | × | |
| 4 | – | 1 | ÷ | 3 | = 1 |
=
1 | | =
12 | | =
45 | |
The product of the numbers in the red boxes is 336.
15 December
The number 2268 is equal to the product of a square number (whose last digit is not 0) and the same square number with its digits reversed:
36×63.
What is the smallest three-digit number that is equal to the product of a square number (whose last digit is not 0) and the same square number with its digits reversed?
Show answer
Hide answer
The only three-digit number that is equal to the product of a square number and the same square number with its digits reversed is 16×61 = 976.
14 December
153 is 3375. The last 3 digits of 153 are 375.
What are the last 3 digits of 151234567890?
Show answer
Hide answer
We can look at the first few powers and look for a pattern:
| n | 15n | Last 3 digits of 15n |
| 1 | 15 | 15 |
| 2 | 225 | 225 |
| 3 | 3375 | 375 |
| 4 | 50625 | 625 |
| 5 | 759375 | 375 |
| 6 | 11390625 | 625 |
| 7 | 170859375 | 375 |
| 8 | 2562890625 | 625 |
| 9 | 38443359375 | 375 |
If n is even (and > 2), the last two digits of 15n are 625.
13 December
Today's number is given in this crossnumber. No number in the completed grid starts with 0.
|
|
| Across |
| 1 | Today's number. | (3) |
| 4 | Two times 5A. | (3) |
| 5 | A multiple of 1. | (3) |
|
| Down |
| 1 | Sum of digits is 15. | (3) |
| 2 | Sum of digits is 19. | (3) |
| 3 | Three times 5A. | (3) |
|
Show answer
Hide answer
As 3D is 3 times 5A, and they both share a final digit, their final digit must be 5 or 0.
If it were 0, then 4A would also end zero, so 3D ends in 00. This would mean that 5A also ends 00. 2D therefore would end in 0, but then it's impossible for the sum of 2D's digits to be 19.
Hence, the final digit of 5A cannot be 0, so must be 5:
As 4A is 2 times 5A, it ends in a 0:
3D is a multiple of 3, so must be 105, 405, or 705. These would mean 5A is 35, 135, or 235 (respectively). 5A has three digits so this rules out the first option. Both other options end in 35:
4A is 2 times 5A, so must end in 70:
The sum of the digits of 2D is 19:
If 5A were 135, then 4A would be 270. But then 1D ends with 21 and its digits cannot add to 15. Therefore 5A 235:
4A is 2 times 5A and 3D is 3 times 5A:
The sum of the digits of 1D is 15:
Therefore, today's number is 997.