Puzzles
Square deal
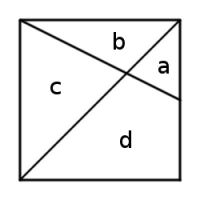
This unit square is divided into four regions by a diagonal and a line that connects a vertex to the midpoint of an opposite side. What are the areas of the four regions?
Show answer & extension
Hide answer & extension
The square is unit, so \(a+b+c+d=1\). By the definitions of the lines, \(a+d=\frac{1}{2}\) and \(a+b=\frac{1}{4}\).
\(a\) and \(c\) are similar triangles. The vertical side of \(c\) is twice that of \(a\) so \(c=4a\).
Therefore we have the system of simultaneous equations:
$$a+b+c+d=1\\a+d=\frac{1}{2}\\a+b=\frac{1}{4}\\c=4a$$
These can be solved to find:
$$a=\frac{1}{12}\\b=\frac{1}{6}\\c=\frac{1}{3}\\d=\frac{5}{12}\\$$
Extension
What would be the areas if the lines were a diagonal and another line which divides the sides in the ratio \(x:y\)?
Light work
"I don't know if you are fond of puzzles, or not. If you are, try this. ... A gentleman (a nobleman let us say, to make it more interesting) had a sitting-room with only one window in it—a square window, 3 feet high and 3 feet wide. Now he had weak eyes, and the window gave too much light, so (don't you like 'so' in a story?) he sent for the builder, and told him to alter it, so as only to give half the light. Only, he was to keep it square—he was to keep it 3 feet high—and he was to keep it 3 feet wide. How did he do it? Remember, he wasn't allowed to use curtains, or shutters, or coloured glass, or anything of that sort."
Chessboard squares
It was once claimed that there are 204 squares on a chessboard. Can you justify this claim?
Show answer & extension
Hide answer & extension
There are 64 1×1 squares, 49 2×2 squares, 36 3×3 squares, 25 4×4 squares, 16 5×5 squares, 9 6×6 squares, 4 7×7 squares and 1 8×8 square on a chessboard.
This can be shown by counting how many positions the top left corner of the square can sit on. For example, the top left corner of a 5×5 square can be in the first four rows and columns of the board (otherwise the square will go off the board) and 4×4=16.
64+49+36+25+16+9+4+1=204.
Extension
How many rectangles are there on a chessboard?
Equal areas
An equilateral triangle and a square have the same area. What is the ratio of the perimeter of the triangle to the perimeter of the square?
Show answer & extension
Hide answer & extension
Let \(A\) be the area of the square (and the triangle).
The length of a side of the square is \(\sqrt{A}\), so the perimeter of the square is \(4\sqrt{A}\).
Let \(l\) be the length of a side the triangle. Then \(\frac{1}{2}l^2\sin{60}=A\), so \(l^2=\frac{4A}{\sqrt{3}}\). Therefore \(l=\frac{2\sqrt{A}}{3^\frac{1}{4}}\) and the perimeter of the triangle is \(\frac{6\sqrt{A}}{3^\frac{1}{4}}\).
Hence the ratio of the perimeters is \(\frac{6\sqrt{A}}{3^\frac{1}{4}} : 4\sqrt{A}\) which simplifies to 33/4:2
Extension
If an \(n\) sided regular polygon has the area \(A\), what is the length of one of its sides?