Puzzles
Integer part
Let \(\lfloor x\rfloor \) denote the integer part of \(x\) (eg. \(\lfloor 7.8\rfloor =7\)).
When are the following true:
a) \(\lfloor x+1\rfloor = \lfloor x\rfloor + 1\)
b) \(\lfloor nx\rfloor = n\lfloor x\rfloor\) (where \(n\) is an integer)
c) \(\lfloor x+y\rfloor = \lfloor x\rfloor +\lfloor y\rfloor \)
d) \(\lfloor xy\rfloor = \lfloor x\rfloor \lfloor y\rfloor \)
Show answer & extension
Hide answer & extension
a) Always
b) When \(n<\frac{1}{f_x}\), where \(f_x\) is the fractional part of \(x\).
c) When the fractional parts of \(x\) and \(y\) add up to less than one.
d) Let \(f_x\) and \(f_y\) be the fractional parts of \(x\) and \(y\) (respectively).
$$\lfloor xy\rfloor = \lfloor (\lfloor x\rfloor +f_x)(\lfloor y\rfloor +f_x)\rfloor $$
$$=\lfloor \lfloor x\rfloor \lfloor y\rfloor +f_x\lfloor y\rfloor +f_y\lfloor x\rfloor +f_yf_x\rfloor $$
$$=\lfloor x\rfloor \lfloor y\rfloor +\lfloor f_x\lfloor y\rfloor +f_y\lfloor x\rfloor +f_yf_x\rfloor $$
This will be equal to \(\lfloor x\rfloor \lfloor y\rfloor \) when \(\lfloor f_x\lfloor y\rfloor +f_y\lfloor x\rfloor +f_yf_x\rfloor =0\).
For this to be true, it is necessary (but not sufficient) that \(f_y<\frac{1}{x}\) and \(f_x<\frac{1}{y}\).
Extension
Show that
$$\lfloor x\rfloor +\left\lfloor x+\frac{1}{n}\right\rfloor +\left\lfloor x+\frac{2}{n}\right\rfloor +...+\left\lfloor x+\frac{n-1}{n}\right\rfloor =\lfloor nx\rfloor.$$
Make the sums
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, \(4+3\times2\) is 14, not 10.
| + | | - | | = 4 |
| + | | - | | × | |
| - | | × | | = 27 |
| - | | × | | ÷ | |
| × | | ÷ | | = 16 |
=
2 | | =
8 | | =
6 | |
Show answer & extension
Hide answer & extension
| 1 | + | 5 | - | 2 | = 4 |
| + | | - | | × | |
| 7 | - | 4 | × | 9 | = 27 |
| - | | × | | × | |
| 6 | × | 8 | - | 3 | = 16 |
=
2 | | =
8 | | =
6 | |
Extension
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct.
| + | | - | | = 5 |
| - | | - | | - | |
| + | | ÷ | | = 5 |
| + | | ÷ | | × | |
| + | | × | | = 99 |
=
0 | | =
1 | | =
18 | |
Rotating round table
At a large dinner, 24 people are to sit evenly spaced around a round table. Place cards are laid to show where everyone should sit. Unfortunately nobody notices the name cards and the guests sit down with nobody in the correct seat.
Show that it is possible to rotate the table so that at least two people will be in the correct seats.
Show answer & extension
Hide answer & extension
Let \(p(n)\) denote the number of people in the correct seat when the table is rotated by \(n\) people. From the question, we know that:
$$p(0)=0$$
As every guest can be put into the correct place by one rotation, we know that:
$$p(0)+p(1)+...+p(23)=24$$
As \(p(0)=0\):
$$p(1)+...+p(23)=24$$
This sum has 23 positive integers adding up to 24, so one of the rotations must lead to at least two people being in the correct places.
Extension
If the 24 guests sat randomly and one person was in the correct seat, could you still rotate the table so that two people are correctly seated?
121
Find a number base other than 10 in which 121 is a perfect square.
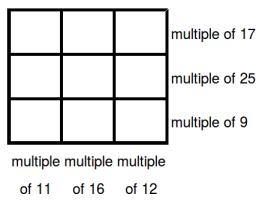
Fill in the digits
Can you place the digits 1 to 9 in the boxes so that the three digit numbers formed in the top, middle and bottom rows are multiples of 17, 25 and 9 (respectively); and the three digit numbers in the left, middle and right columns are multiples of 11, 16 and 12 (respectively)?
The taxman
In a very strange country, the tax system works as follows.
£1, £2, £3 up to £12 are available.
You pick an amount. You keep this amount, but the taxman takes any factors of it. You cannot pick any amount without a factor.
This continues until you can take no more money. The taxman gets any remaining money.
For example, you might play as follows:
- Take £12. Taxman gets £1, £2, £3, £4, £6.
- Take £10. Taxman gets £5.
- You cannot take anything. Taxman gets £7, £8, £9, £11.
In this example, you end with £22 and the taxman ends with
£56.
Is it possible to get more money than the taxman? What is the most you can get?
Show answer & extension
Hide answer & extension
The maximum you can get is £50, with the taxman getting
£28. Here is
how to get it:
- Take £11. Taxman gets £1.
- Take £9. Taxman gets £3.
- Take £8. Taxman gets £2, £4.
- Take £10. Taxman gets £5.
- Take £12. Taxman gets £6.
- You cannot take anything. Taxman gets £7.
Extension
Can you always beat the taxman if £1 up to £\(n\) are
available?
One hundred factorial
How many zeros does \(100!\) end with?
Show answer & extension
Hide answer & extension
The number of zeros at the end of a number is the same as the number of 10s in the product that makes the number. Each of these 10s is made by multiplying 5 by 2.
There will be more even numbers than multiples of 5 in \(100!\), so the number of 5s will tell us how many zeros the number ends in.
In \(100!\), there will be 20 multiples of 5 and 4 multiples of \(5^2\). This means that \(100!\) will end in 24 zeros.
Extension
How many zeros will \(n!\) end in?
Products and sums of squares
Show that the product of any two numbers, each of which is the sum of two square integers, is itself the sum of two square integers.
Show answer & extension
Hide answer & extension
The result of the multiplication can be written as:
$$(a^2+b^2)(c^2+d^2)$$
where \(a\), \(b\), \(c\) and \(d\) are integers. Expanding the brackets gives:
$$a^2c^2+b^2c^2+a^2d^2+b^2d^2$$
Next, if \((bd-ac)^2\) and \((bc+ad)^2\) are expanded, we get:
$$(bd-ac)^2=b^2d^2+a^2c^2-2abcd$$
$$(bc+ad)^2=b^2c^2+a^2d^2+2abcd$$
And so:
$$(a^2+b^2)(c^2+d^2)=(bd-ac)^2+(bc+ad)^2$$
We have written the product as the sum of two integers.
Extension
For which integers \(a\), \(b\), \(c\) and \(d\) can the result \((a^2+b^2)(c^2+d^2)\) be written as the sum of two square integers in more than one way?