Puzzles
18 December
Some numbers can be written as the product of two or more consecutive integers, for example:
$$6=2\times3$$
$$840=4\times5\times6\times7$$
What is the smallest three-digit number that can be written as the product of two or more consecutive integers?
15 December
The arithmetic mean of a set of \(n\) numbers is computed by adding up all the numbers, then
dividing the result by \(n\).
The geometric mean of a set of \(n\) numbers is computed by multiplying all the numbers together, then
taking the \(n\)th root of the result.
The arithmetic mean of the digits of the number 132 is \(\tfrac13(1+3+2)=2\).
The geometric mean of the digits of the number 139 is \(\sqrt[3]{1\times3\times9}\)=3.
What is the smallest three-digit number whose first digit is 4 and for which the arithmetic and geometric means of its digits are both non-zero integers?
Show answer & extension
Hide answer & extension
The only three digit number whose first digits is 4 and for which the arithmetic and geometric means of its digits are both non-zero integers is 444.
Extension
How many three digit numbers are there for which the arithmetic and geometric means of its digits are both non-zero integers?
How many four digit numbers are there for which the arithmetic and geometric means of its digits are both non-zero integers?
12 December
What is the smallest value of \(n\) such that
$$\frac{500!\times499!\times498!\times\dots\times1!}{n!}$$
is a square number?
Show answer
Hide answer
Consider the first two terms in the product:
$$
500!\times499!
=500\times499!\times499!$$
$$= 500\times(499!)^2.$$
Doing similar steps with each pair of terms in the product, we see that:
$$
500!\times499!\times498!\times\dots\times1!
=
500\times498\times\dots\times2\times(499!\times497!\times\dots\times1!)^2
$$
$$
=
(2\times250)\times(2\times249)\times\dots\times(2\times1)\times(499!\times497!\times\dots\times1!)^2
$$
$$
=
2^{250}\times250!\times(499!\times497!\times\dots\times1!)^2
$$
If we divide this by \(250!\), we are left with a square number, and so \(n\) is 250
11 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | + | | = 15 |
| + | | + | | ÷ | |
| + | | – | | = 10 |
| + | | – | | × | |
| ÷ | | × | | = 3 |
=
16 | | =
1 | | =
30 | |
Show answer
Hide answer
| 3 | + | 7 | + | 5 | = 15 |
| + | | + | | ÷ | |
| 9 | + | 2 | – | 1 | = 10 |
| + | | – | | × | |
| 4 | ÷ | 8 | × | 6 | = 3 |
=
16 | | =
1 | | =
30 | |
The product of the numbers in the red boxes is 120.
10 December
How many integers are there between 100 and 1000 whose digits add up to an even number?
Show answer
Hide answer
Between 100 and 109 (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number.
Between 110 and 119 (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number...
In general, between \(10n\) and \(10n+9\) (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number.
The integers from 100 to 999 (inclusive) can be split into 45 sets of integers from \(10n\) to \(10n+9\) (and the digits of 1000 don't add to an even number), so there are
450 integers between 100 and 1000 whose digits add up to an even number.
8 December
Noel writes the numbers 1 to 17 in a row. Underneath, he writes the same list without the first and last numbers, then continues this until he writes a row containing just one number:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| | | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | | |
| etc. |
What is the sum of all the numbers that Noel has written?
6 December
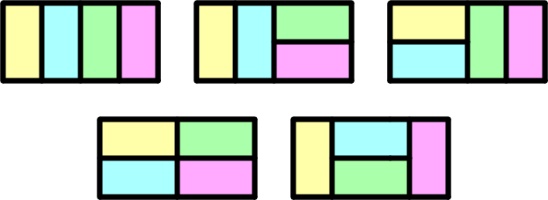
There are 5 ways to tile a 4×2 rectangle with 2×1 pieces:
How many ways are there to tile a 12×2 rectangle with 2×1 pieces?
Show answer
Hide answer
Let \(a_n\) be the number of ways to tile a \(n\times2\) rectangle.
It is easy to check that \(a_1=1\) (ie there is 1 way to tile a 1×2 rectangle) and \(a_2=2\) (ie there are 2 ways to tile a 2×2 rectangle).
For an \(n\times2\) rectangle, from the left the tiling either starts with a vertical tile, or a pair of horizontal tiles.
If it starts with a vertical tile, then there are \(a_{n-1}\) ways to tile the remaining \((n-1)\times2\) rectangle.
If it starts with a pair of horizontal tile2, then there are \(a_{n-2}\) ways to tile the remaining \((n-2)\times2\) rectangle.
Therefore, \(a_n=a_{n-1}+a_{n-2}\).
(And so the number of ways to tile a \(n\times2\) rectangle is the \((n+1)\)th Fibonacci number.)
Therefore, the number of ways to tile a 12×2 rectangle is 233.
5 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | + | | = 15 |
| + | | – | | + | |
| + | | + | | = 15 |
| + | | × | | ÷ | |
| + | | + | | = 15 |
=
15 | | =
15 | | =
15 | |
Show answer
Hide answer
| 2 | + | 6 | + | 7 | = 15 |
| + | | – | | + | |
| 4 | + | 3 | + | 8 | = 15 |
| + | | × | | ÷ | |
| 9 | + | 5 | + | 1 | = 15 |
=
15 | | =
15 | | =
15 | |
The product of the numbers in the red boxes is 378.