Puzzles
Subsum
1) In a set of three integers, will there always be two integers whose sum is even?
2) How many integers must there be in a set so that there will always be three integers in the set whose sum is a multiple of 3?
3) How many integers must there be in a set so that there will always be four integers in the set whose sum is even?
4) How many integers must there be in a set so that there will always be three integers in the set whose sum is even?
Fill in the digits
Source: Chalkdust
![](javascript:showlimage("chalkdust-puzzle.png"))
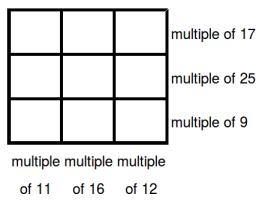
Can you place the digits 1 to 9 in the boxes so that the three digit numbers formed in the top, middle and bottom rows are multiples of 17, 25 and 9 (respectively); and the three digit numbers in the left, middle and right columns are multiples of 11, 16 and 12 (respectively)?
Always a multiple?
Source: nrich
Take a two digit number. Reverse the digits and add the result to your original number. Your answer is multiple of 11.
Prove that the answer will be a multiple of 11 for any starting number.
Will this work with three digit numbers? Four digit numbers? \(n\) digit numbers?